Preprints and publications in reverse chronological order:
-
Kantorovich Duality for Some Topologically Degenerate Zero-One Costs
with Daniel Raban.
In progress (2024+).
-
Nearly-Maximal Germ Couplings of Lévy Processes
with Yang Chu.
In progress (2024+).
-
Fréchet Means in Infinite Dimensions.
In progress (2024+).
[abstract]
- While there exists an emerging probabilistic theory of Fréchet means in a general "finite-dimensional" setting, there also exist a few notable results in particular "infinite-dimensional" settings of interest.
Presently, we introduce a geometric condition for a general infinite-dimensional setting under which one can prove a continuity result that implies several probabilistic limit theorems of interest.
We also reduce the moment assumptions from the existing literature to the provably minimal possible.
We conclude by proving novel results or strengthening existing results in three applications: metric projections in approximation theory, Wasserstein barycenters in optimal transport, and image processing in pattern theory.
-
Large Deviations Principle for Bures-Wasserstein Barycenters
with Leonardo Santoro.
In progress (2024+).
-
Strong Consistency for a Class of Adaptive Clustering Procedures.
Under review at Annals of Statistics (2024+).
[abstract]
[arxiv]
- We introduce a class of clustering procedures which includes \(k\)-means and \(k\)-medians, as well as variants of these where the number of cluster centers can be chosen adaptively (for example, according to the elbow method) and where the domain of the cluster centers can be chosen adaptively (for example, \(k\)-medoids).
In the non-parametric setting and assuming only the finiteness of certain moments, we show that all clustering procedures in this class are strongly consistent under independent, identically-distributed samples.
In the adaptive setting, our work provides a strong consistency result that is the first of its kind.
In the non-adaptive setting, our work strengthens many existing results in the literature by providing a robust method of proof which allows one to prove further limit theorems.
-
Fréchet Mean Set Estimation in the Hausdorff Metric, via Relaxation with Moïse Blanchard.
To appear in Bernoulli (2024+).
[abstract]
[arxiv]
- This work resolves the following question in non-Euclidean statistics: Is it possible to consistently estimate the Fréchet mean set of an unknown population distribution, with respect to the Hausdorff metric, when given access to independent identically-distributed samples?
Our affirmative answer is based on a careful analysis of the "relaxed empirical Fréchet mean set estimators" which identify the set of near-minimizers of the empirical Fréchet functional and where the amount of "relaxation" vanishes as the number of data tends to infinity.
Our main theoretical results include exact descriptions of which relaxation rates give weak consistency and which give strong consistency, as well as the construction of a "two-step estimator" which (assuming only the finiteness of certain moments and a mild condition on the metric entropy of the underlying metric space) adaptively finds the fastest possible relaxation rate for strongly consistent estimation.
Our main practical result is simply that researchers working with non-Euclidean data in the real world can be better off computing relaxed empirical Fréchet mean sets rather than unrelaxed empirical Fréchet mean sets.
-
Constructing Maximal Germ Couplings of Brownian Motions with Drift with Sebastian Hummel.
Electronic Communications in Probability. 29, 1-11.
[abstract]
[animation]
[arxiv]
[journal]
-
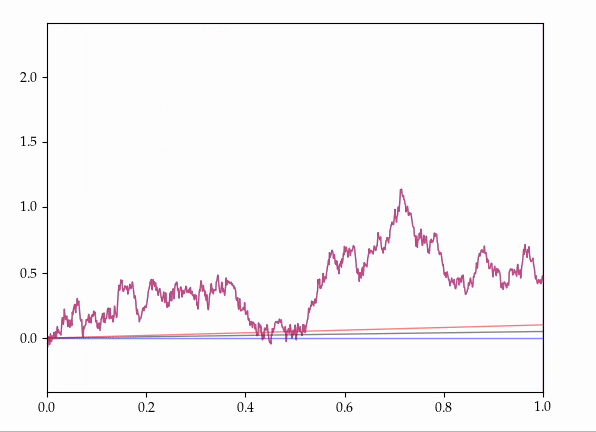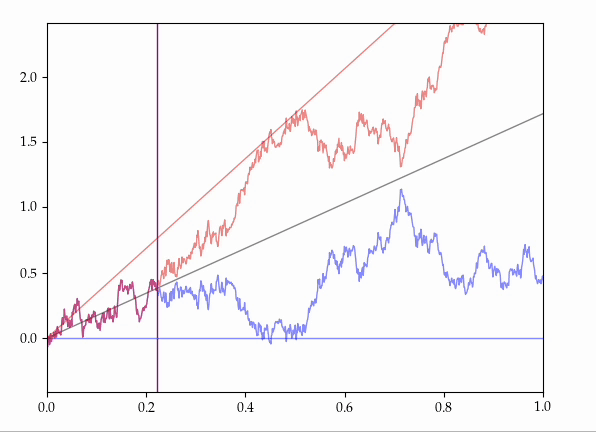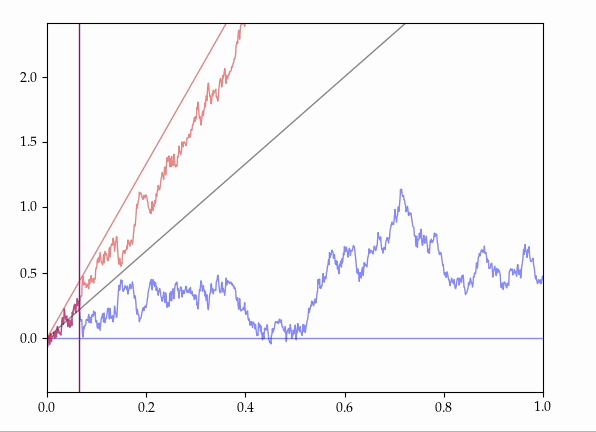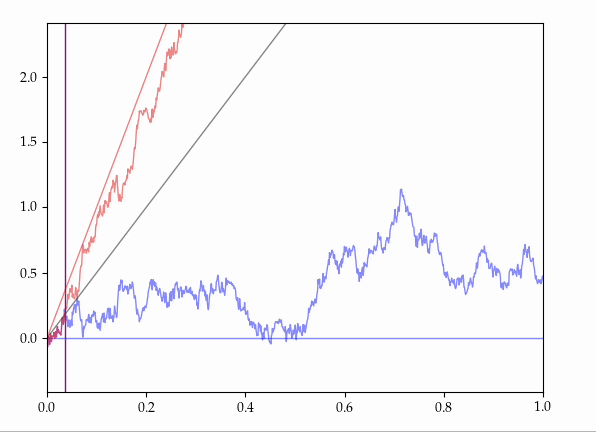
- Consider all the possible ways of coupling together two Brownian motions with the same starting position but with different drifts onto the same probability space.
It is known that there exist couplings which make these processes agree for some random, positive, maximal initial length of time.
Presently, we provide an explicit, elementary construction of such couplings.
-
Limit Theorems for Fréchet Mean Sets with Steve N. Evans.
Bernoulli. 30(1), 419-447.
[abstract]
[arxiv]
[journal]
- For \(1\le p \le \infty\), the Fréchet \(p\)-mean of a probability measure on a metric space is an important notion of central tendency that generalizes the usual notions in the real line of mean (\(p=2\)) and median (\(p=1\)).
In this work we prove a collection of limit theorems for Fréchet means and related objects, which, in general, constitute a sequence of random closed sets.
On the one hand, we show that many limit theorems (a strong law of large numbers, an ergodic theorem, and a large deviations principle) can be simply descended from analogous theorems on the space of probability measures via purely topological considerations.
On the other hand, we provide the first sufficient conditions for the strong law of large numbers to hold in a \(T_2\) topology (in particular, the Fell topology), and we show that this condition is necessary in some special cases.
We also discuss statistical and computational implications of the results herein.
-
A Strong Duality Principle for Equivalence Couplings and Total Variation.
Electronic Journal of Probability. 28, 1-33
[abstract]
[arxiv]
[journal]
- We introduce and study a notion of duality for two classes of optimization problems commonly occurring in probability theory.
That is, on an abstract measurable space \((\Omega,\mathcal{F})\), we consider pairs \((E,\mathcal{G})\) where \(E\) is an equivalence relation on \(\Omega\) and \(\mathcal{G}\) is a sub-\(\sigma\)-algebra of \(\mathcal{F}\); we say that \((E,\mathcal{G})\) satisfies "strong duality" if \(E\) is \((\mathcal{F}\otimes\mathcal{F})\)-measurable and if for all probability measures \(\mathbb{P},\mathbb{P}'\) on \((\Omega,\mathcal{F})\) we have
\[
\max_{A\in\mathcal{G}}\vert \mathbb{P}(A)-\mathbb{P}'(A)\vert = \min_{\tilde{\mathbb{P}}\in\Pi(\mathbb{P},\mathbb{P}')}(1-\tilde{\mathbb{P}}(E)),
\]
where \(\Pi(\mathbb{P},\mathbb{P}')\) denotes the space of couplings of \(\mathbb{P}\) and \(\mathbb{P}'\), and where
"max" and "min" assert that the supremum and infimum are in fact achieved.
The results herein give wide sufficient conditions for strong duality to hold, thereby extending a form of Kantorovich duality to a class of cost functions which are irregular from the point of view of topology but regular from the point of view of descriptive set theory.
The given conditions recover or strengthen classical results, and they have novel consequences in stochastic calculus, point process theory, and random sequence simulation.
-
Virtual Markov Chains with Steve N. Evans.
New Zealand Journal of Mathematics (Vaughan Jones Memorial Special Issue). 52, 511–559.
[abstract]
[arxiv]
[journal]
- We introduce the space of virtual Markov chains (VMCs) as a projective limit of the spaces of all finite state space Markov chains (MCs), in the same way that the space of virtual permutations is the projective limit of the spaces of all permutations of finite sets. We introduce the notions of virtual initial distribution (VID) and a virtual transition matrix (VTM), and we show that the law of any VMC is uniquely characterized by a pair of a VID and VTM which have to satisfy a certain compatibility condition. Lastly, we study various properties of compact convex sets associated to the theory of VMCs, including that the Birkhoff-von Neumann theorem fails in the virtual setting.
