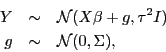

Next: Standard errors in gam(),
Up: Spatial and spatio-temporal data
Previous: Space-time smoothing in R
If you're interested in fitting a model,
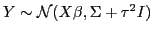 ,
where
,
where 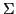 captures correlation, such as spatial structure, you
have two options. I prefer likfit() for two reasons. First
it can make use of the Matérn covariance. Second it seems to do
a much better maximization job, often finding higher likelihoods than
gls().
captures correlation, such as spatial structure, you
have two options. I prefer likfit() for two reasons. First
it can make use of the Matérn covariance. Second it seems to do
a much better maximization job, often finding higher likelihoods than
gls().
- Use gls() from the nlme package in R. The 'exponential'
and 'Gaussian' correlation functions are two options. Make sure to
include the nugget. Note that 'sig2' is the total variation
and 'nugget' is the proportion for the spatial component
(I think - I haven't checked this recently).
gls(y~x,correlation=corExp(form=~xs1+xs2,nugget=TRUE),method='ML')
- Use likfit() from the geoR package in R. Here trend.spatial
specifies the mean term. kappa is the Matérn differentiability
parameter.
likfit(coords=xs,data=y,ini.cov.pars=c(0.4,0.4),fix.kappa=T,kappa=2,cov.model='matern',trend=trend.spatial(~x),messages=F,method.lik='ML')
Note that the model above is the same as a model
namely a spatial random effects or Gaussian process-based model.
Last modified: 12/14/08. Typo corrected 1/14/12.
Chris Paciorek
2012-01-21
![]() ,
where
,
where ![]() captures correlation, such as spatial structure, you
have two options. I prefer likfit() for two reasons. First
it can make use of the Matérn covariance. Second it seems to do
a much better maximization job, often finding higher likelihoods than
gls().
captures correlation, such as spatial structure, you
have two options. I prefer likfit() for two reasons. First
it can make use of the Matérn covariance. Second it seems to do
a much better maximization job, often finding higher likelihoods than
gls().