Introduction
History
Surveys
Generalizations
Specializations
Related subjects
Applications
Bibliography
|
The Galton-Watson process, deriving from Galton's study of extinction
of family names, is a discrete-generation process parametrized
by a probability distribution
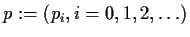 .
Each individual in a generation has a random number of offspring
in the next generation, this number being picked from .
Each individual in a generation has a random number of offspring
in the next generation, this number being picked from 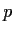 , independently
for different parents.
Three cases are distinguished as follows, according to the mean number
of offspring, , independently
for different parents.
Three cases are distinguished as follows, according to the mean number
of offspring,
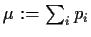
- the subcritical case:
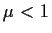
- the critical case:
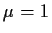
- the supercritical case:
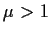 . .
A highlight of elementary theory is that extinction is
certain in the subcritical and critical cases,
whereas survival forever has positive probability in the
supercritical case.
Branching processes, together with queues, provide the
simplest examples of the criticality
or phase transition phenomenon that is of widespread
interest in more complex statistical physics models.
A highlight of classical theory is the Kesten-Stigum theorem,
asserting that in the supercritical case,
where the size  of the of the 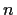 'th generation
satisfies 'th generation
satisfies
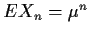 for mean offspring for mean offspring 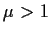 ,
we have a non-degenerate a.s. limit for ,
we have a non-degenerate a.s. limit for 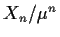 ,
under a ,
under a 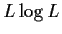 integrability condition. integrability condition.
In a multitype branching process, the individuals
have a type which determines the distribution of number
of types of offspring. With a finite type space, the theory
of multitype branching processes broadly parallels the single-type case.
Continuous-time branching processes can be defined in several
levels of generality.
Envisaging biological populations, one may suppose that an
female has a lifetime and a number of female children born at different
ages; there is an arbitrary distribution on (lifetime, ages at births),
the key assumption being that for each new child there is an independent
pick from the distribution.
This Crump-Mode-Jagers model and its multitype analogs,
in the supercritical case, retain
essential features of the Galton-Watson case:
there is (given nonextinction) exponential growth of population,
with proportions of different type converging to a
deterministic stable type structure.
The essence of classical models is the
independence property of the behavior of new individuals.
and lack of spatial structure.
Other models incorporate further structure,
but the classical theory continues to plays an important role
in their study, for instance by enabling simple comparison arguments.
Such models inlude
- branching random walk in which particles having spatial
position,
- interacting particle systems governed by
various rules for interactions between particles,
- random graphs where the structure of the component
containing a particular vertex can be analyzed by comparison
with a branching process.
A huge number of other variants have been studied,
and around 100 papers per year continue to be published.
For instance, the offspring distribution may be population-size dependent,
or randomly varying in time.
Classical connections with other topics such as
queueing (where arrivals during the service period of
one customer may be identified as offspring of that customer)
and random walk
(where properties of near-critical branching processes may be deduced from
properties of an associated near-critical random walk)
continue to be of interest.
Other connections include
fragmentation processes, in which particles of size 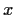 are randomly split into smallers particles of masses summing to
are randomly split into smallers particles of masses summing to 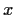 ,
and random recursive fractals, which replace deterministic
constructions of sets like the Sierpinski gasket with randomized constructions.
Although elementary treatments identify the Galton-Watson process
with its generation-size process ,
and random recursive fractals, which replace deterministic
constructions of sets like the Sierpinski gasket with randomized constructions.
Although elementary treatments identify the Galton-Watson process
with its generation-size process
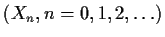 ,
the process is really a particular model of a random tree,
and branching processes often underlie apparently different models
of random tree. ,
the process is really a particular model of a random tree,
and branching processes often underlie apparently different models
of random tree.
|
MathSciNet |
MathGate |
MathSurvey |
LaTeX2HTML |



Next: History
Up: Branching Processes
Previous: Branching Processes
Jim &
2002-12-30
|