S Appendix
S Commands for Problem I
For the value of N decided upon in the first part of this problem,
generate 100 samples of size N from
the exponential distribution and store them in a matrix using the command
X <- matrix(rexp(100*N),100,N)
We are now in a position to calculate values of 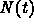 for
for  .
For example, suppose we want to generate 100 random variables from the Poisson
process with mean
.
For example, suppose we want to generate 100 random variables from the Poisson
process with mean  . First we create a matrix cum
where each row of cum contains the cumulative sum of each row of X.
This can be done using the apply command in S. Hence the command we would give would be
. First we create a matrix cum
where each row of cum contains the cumulative sum of each row of X.
This can be done using the apply command in S. Hence the command we would give would be
cum <- t(apply(X,1,cumsum))
In S the command t(A) transposes the matrix A. The reason for
taking the
transpose is that the cumsum function in S when applied to the rows of X
creates columns of the cumulative values of the rows of X.
Then we create an indicator matrix, say, indicat that is of the same size
as X and whose  th element is 1 if X(i,j) is less than or
equal to 5 and 0 otherwise. For this we use the command
th element is 1 if X(i,j) is less than or
equal to 5 and 0 otherwise. For this we use the command
indicat[cum <= 5] <- 1
Finally you get 100 values from the Poisson(5) process by the
following command
Nt <- apply(indicat,1,sum)
which just sums up each row of the matrix indicat.
Nt now contains 100 observations of the random variable  .
Similarly you will get
.
Similarly you will get  for
for  .
To compare the relative frequencies with the theoretical distribution,
you will have to implement a function that generates the probability
vector of a Poisson distribution.
.
To compare the relative frequencies with the theoretical distribution,
you will have to implement a function that generates the probability
vector of a Poisson distribution.
S Help for Section II
- Proceed as above to generate the processes using the
cumsum function to get
 . Calculating
. Calculating  from X can be done using the
commands given in the previous section.
from X can be done using the
commands given in the previous section.
- The 100 values of
 are simply the elements of
the 30th column of X.
are simply the elements of
the 30th column of X.
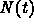 for
for  .
For example, suppose we want to generate 100 random variables from the Poisson
process with mean
.
For example, suppose we want to generate 100 random variables from the Poisson
process with mean  . First we create a matrix cum
where each row of cum contains the cumulative sum of each row of X.
This can be done using the apply command in S. Hence the command we would give would be
. First we create a matrix cum
where each row of cum contains the cumulative sum of each row of X.
This can be done using the apply command in S. Hence the command we would give would be
 th element is 1 if X(i,j) is less than or
equal to 5 and 0 otherwise. For this we use the command
th element is 1 if X(i,j) is less than or
equal to 5 and 0 otherwise. For this we use the command
 .
Similarly you will get
.
Similarly you will get  for
for  .
To compare the relative frequencies with the theoretical distribution,
you will have to implement a function that generates the probability
vector of a Poisson distribution.
.
To compare the relative frequencies with the theoretical distribution,
you will have to implement a function that generates the probability
vector of a Poisson distribution.
 . Calculating
. Calculating  from X can be done using the
commands given in the previous section.
from X can be done using the
commands given in the previous section.
 are simply the elements of
the 30th column of X.
are simply the elements of
the 30th column of X.