Simulation of a Poisson Process on the Real Line
In this section of the lab we will
simulate a Poisson process. Ultimately, we will use such simulations to check
property (iii) of Section 4.5 on page 216 of the text.
Let  be independent random variables
each having the exponential distribution with inverse-scale parameter 1,
and set
be independent random variables
each having the exponential distribution with inverse-scale parameter 1,
and set 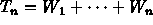 for
for  .
As explained in the text, we think of
.
As explained in the text, we think of  as the failure time of the
ith component once it is installed in a given system.
We assume that the first component is
installed at time zero and that a fresh component is installed as soon as the
one currently installed fails. Then
as the failure time of the
ith component once it is installed in a given system.
We assume that the first component is
installed at time zero and that a fresh component is installed as soon as the
one currently installed fails. Then
 is the failure
time of the nth component that is installed.
For
is the failure
time of the nth component that is installed.
For 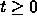 , we will let
, we will let  be the
number of components that have been installed and failed by time t.
be the
number of components that have been installed and failed by time t.
- Suppose we are interested in following the process up to time
t=10.
We first need to decide upon a practical
upper limit N so that with high probability
 is larger than 10.
Use the fact that
is larger than 10.
Use the fact that  has a gamma distribution to find a value of
N such that
has a gamma distribution to find a value of
N such that  .
.
- For the above value of N, generate 100 samples of size N from
the exponential distribution. Use these samples to produce 100 simulated
Poisson processes. Make a scatterplot of
 versus t
for three of these simulated processes (for
versus t
for three of these simulated processes (for  ).
).
- Use the above simulations to generate 100 observations of
 and
and  and draw a histogram for each.
Does the relative frequency of the
numbers
and draw a histogram for each.
Does the relative frequency of the
numbers  support the theoretical
distribution of
support the theoretical
distribution of  ?
Now, consider the 100 observations of
?
Now, consider the 100 observations of  .
Once again, does
the relative frequency of the
numbers
.
Once again, does
the relative frequency of the
numbers  support the theoretical results given in the text
about the distribution of
support the theoretical results given in the text
about the distribution of  ?
?
 be independent random variables
each having the exponential distribution with inverse-scale parameter 1,
and set
be independent random variables
each having the exponential distribution with inverse-scale parameter 1,
and set 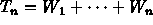 for
for  .
As explained in the text, we think of
.
As explained in the text, we think of  as the failure time of the
ith component once it is installed in a given system.
We assume that the first component is
installed at time zero and that a fresh component is installed as soon as the
one currently installed fails. Then
as the failure time of the
ith component once it is installed in a given system.
We assume that the first component is
installed at time zero and that a fresh component is installed as soon as the
one currently installed fails. Then
 is the failure
time of the nth component that is installed.
For
is the failure
time of the nth component that is installed.
For 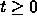 , we will let
, we will let  be the
number of components that have been installed and failed by time t.
be the
number of components that have been installed and failed by time t.
 is larger than 10.
Use the fact that
is larger than 10.
Use the fact that  has a gamma distribution to find a value of
N such that
has a gamma distribution to find a value of
N such that  .
.
 versus t
for three of these simulated processes (for
versus t
for three of these simulated processes (for  ).
).
 and
and  and draw a histogram for each.
Does the relative frequency of the
numbers
and draw a histogram for each.
Does the relative frequency of the
numbers  support the theoretical
distribution of
support the theoretical
distribution of  ?
Now, consider the 100 observations of
?
Now, consider the 100 observations of  .
Once again, does
the relative frequency of the
numbers
.
Once again, does
the relative frequency of the
numbers  support the theoretical results given in the text
about the distribution of
support the theoretical results given in the text
about the distribution of  ?
?