- Consider two events, A and B. Suppose that P(A) = 90% and
P(B) = 60%.
i. A and B cannot be mutually exclusive.
ii. A and B cannot be independent.
a) i is true, ii is false.
b) i is false, ii is true.
c) both i and ii are true.
d) both i and ii are false.
e) There is not enough information to answer this
question.
- E. Taub, M. Munz, and R.R. Tasker, ("Chronic
electrical stimulation of the gasserian ganglion for the
relief of pain in a series of 34 patients," J.
Neurosurg. 86, 197-202, 1997) report on the
effectiveness of surgically implanted electrodes for
reducing facial pain. 34 patients with "chronic
medically intractable facial pain" underwent the
procedure; 19 of the cases (56%) were deemed successful,
in the sense that "there was a reduction of pain by
at least 50% whenever the stimulator was on." Those
19 received permanent implants; 7 of them subsequently
developed infections. Let's ignore the issue of assessing
subjective pain relief, and concentrate on the design.
a) This is an observational study.
b) This is an experiment.
c) This is a controlled experiment.
d) This is a randomized, controlled experiment.
e) None of the above.
- With reference to the question about treating facial pain
with electrical stimulation:
i) The placebo effect is not likely to be a confounding
factor in this design.
ii) The fact that the surgeons knew who had received
treatment is likely to be a confounding factor in this
design.
a) i is true, ii is false.
b) i is false, ii is true.
c) Both i and ii are true.
d) Both i and ii are false.
- Garrison Keillor, the host of the radio show "A
Prairie Home Companion," tells stories about his
hometown, Lake Wobegon, MN, "where all the women are
strong, all the men are good looking, and all the
children are above average." This must be a
fictitious place because:
a) Norwegian bachelor farmers aren't that good looking.
b) Only half the children in any town can be above
average.
c) People from Minnesota aren't any stronger,
better-looking, or smarter than the rest of us.
d) In any reasonably large sample of people, such as a
town, there's bound to be a weak woman, an unattractive
man, or an unintelligent child.
e) None of the above.
- A "full house" in poker is three of one kind
and a pair of another kind; for example, the Ace of
Spades, Ace of Hearts, Ace of Clubs, 2 of Diamonds and 2
of Clubs. Assuming that five cards are dealt from a
well-shuffled, standard, 52-card deck, the chance that
the five cards are a "full house" is
a) 13C2 × 4C2
× 4C3/52C5.
b) 13 × 12 × 4C2
× 4C3/52C5.
c) 13C2 × 45/52C5.
d) 13C1 × 12C1
× 45 × /52C5.
e) 52C2 × 45/52C5.
- The area under the normal curve between +1 and +2 is
closest to
(a) 6%. (b) 14%. (c) 28%. (d) 32%. (e)
48%.
-
Suppose that in a certain group of married couples,
the average IQ of men and of women is 100 points, the SD
of IQ of men and of women is 15 points, and the
correlation coefficient between the IQ's of wives and
husbands is 0.8. The scatterplot of IQ's is
football-shaped. The regression line prediction of the
average IQ of men married to women whose IQ is 120 points
is closest to
a) 125 points.
b) 120 points.
c) 115 points.
d) 110 points.
e) cannot be determined from the information given.
- This refers to the question about the IQs of married
couples. The rms error of regression is closest to
a) 15 points.
b) 12 points.
c) 9 points.
d) 6 points.
e) cannot be determined from the information given.
- This refers to the question about the IQs of married
couples. The 84th percentile of the IQ of men married to
women whose IQ is 120 is closest to
a) 130 points.
b) 125 points.
c) 120 points.
d) 115 points.
e) cannot be determined from the information given.
- This refers to the question about the IQs of married
couples.
i) Because of regression towards the mean, the woman with
the highest IQ will be married to a man whose IQ is lower
than hers.
ii) In spite of regression towards the mean, the woman
with the highest IQ is likely to be married to a man
whose IQ is even higher than hers, because smart men
don't like to marry women who are smarter than they are.
iii) Because of regression towards the mean, a child of
the woman with the highest IQ (assuming she has children)
is likely to have an IQ that is above average, but not as
high as hers.
a) i is true; ii and iii are false.
b) i and iii are true; ii is false.
c) ii is true; i and iii are false.
d) ii and iii are true; i is false.
e) iii is true; i and ii are false.
- In the following sketch of a scatterplot, the slanting
line is
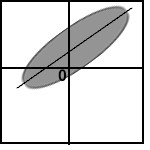
a) The graph of averages.
b) The SD line.
c) The regression line of Y on X.
d) The regression line of X on Y.
e) None of the above.
- Y. Zhang et al., in "Bone mass and the risk
of breast cancer among postmenopausal women," New
England J. Medicine, 336, 611-617, 1997, report on
the incidence of breast cancer among 1373 women who had
had hand X-rays between 1967 and 1970, had not had breast
cancer at that time, and were age 47-80 at that time. The
area of one of the bones in their wrists was measured
from the X-ray images. The women were followed until
1993. By that time, 91 of the subjects had developed
breast cancer. In analyzing the data, the scientists
divided the women into two-year age groups to control for
the effect of age on bone area (people tend to lose bone
mass after maturity). They also tried to control for
education, height, body mass, age at first pregnancy,
parity (number of children), age at menopause, alcohol
consumption, cigarette smoking, level of physical
activity, and use of postmenopausal estrogen, on the
incidence of breast cancer, with which all of these
factors have been associated. (They do this
"controlling" using a multivariate regression
model, which we shall not question here.) After adjusting
for these other factors, there was an association between
bone area and the incidence of breast cancer: the
incidence of breast cancer among women in the top
quartile of bone area (adjusted for age) was about 3.5
times higher than the incidence among women in the bottom
quartile. There is a known positive association between
long-term postmenopausal estrogen exposure and retention
of bone mass, and there is a known positive association
between estrogen level at a given time and breast cancer.
a) Because this is a longitudinal study, the effects of
confounding should be reduced.
b) Because this is a cross-sectional study, age is likely
to be confounded with other factors.
c) This study provides evidence that long-term estrogen
exposure increases the risk of breast cancer.
d) (a) and (c) are true.
e) None of the above is true.
Below are sketches of residual plots from four
regressions. Characterize each plot by one of the
following letters, according to whether the plot reveals
(a) something's wrong with the regression
(b) residuals are heteroscedastic
(c) relationship is nonlinear
(d) heteroscedastic and nonlinear
(e) everything's fine
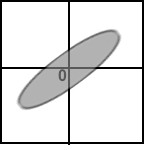 a.
a.
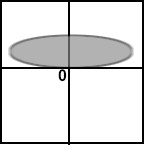 a.
a.
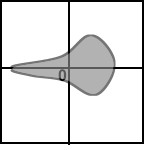 b.
b.
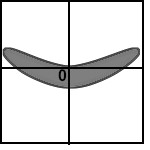 c.
c.
- The points on a scatterplot of two variables lie exactly
on a straight line with slope -2. The point of averages
is (-1,1). The correlation between the two variables is
(a) -2, (b) -1, (c) 1/2, (d) 1, (e) not
enough information.
- In the previous question, the equation of the regression
line for regressing Y on X is:
(a) y=2x, (b) y = -2x - 1, (c) y = -x/2, (d)
y = -2x, (e) not enough information.
The next six questions refer to the list {0, 1, 3, 0, -3,
-1}.
- The mean is: (a) 1/6, (b) 1/3, (c) 1, (d) 0,
(e) none of the above.
- The median is: (a) -1, (b) 0, (c) 1, (d)
2, (e) none of the above.
- The RMS is: (a) sqrt(5), (b) sqrt(3 1/3),
(c) sqrt(20), (d) 2, (e) none of the above.
- The SD is: (a) sqrt(22/6), (b) sqrt(5), (c)
sqrt(3 1/3), (d) sqrt(20) (e) none of the above.
- The 25th percentile is: (a) -3, (b) -1,
(c) 0, (d) 1, (e) none of the above.
- The inter-quartile range is: (a) -1 to 1, (b) 2,
(c) -1 to 3, (d) 4, (e) none of the above.
- In 100 trips on the Evans Hall elevator, my average
waiting time was 3 minutes. The number of times I had to
wait more than 15 minutes was no more than (a) 3, (b) 5,
(c) 15, (d) 20, (e) cannot be determined
from this information.

 a.
a. a.
a. b.
b. c.
c.