- Is Statistics something you do to data? Is it procedural?
- Ideally, it's a way of thinking to avoiding fooling yourself & others.
- In many disciplines, "Statistics" is calculation, not thinking.
- Consequence of how statistics is taught and of peverse incentives: Cargo-Cult Statistics.



Problem statement¶
- Want to use data $Y \in \Re^n$ to learn about the (unknown) state of the world, $\theta$ in a mathematical model of physical system.
- Often $\theta$ is a function of position and/or time: infinite-dimensional
- "Know" that $\theta \in \Theta$.
- measurement model: If $\theta = \eta$, $Y \sim P_\eta$.
- Known measure $\mu$ that dominates all $P_\eta$ s.t. $\eta \in \Theta$.
- Density of $P_\eta$ at $y$ w.r.t. $\mu$ is
- likelihood of $\eta$ given $Y = y$ is $p_\eta(y)$, viewed as function of $\eta$.
- Typically impossible to estimate $\theta$ with any useful level of accuracy (maybe not even identifiable).
- Generally possible and scientifically interesting to estimate some parameter $\lambda = \lambda[\theta]$
The Bayesian Approach¶
- Uses prior probability distribution $\pi$ on $\Theta$ and likelihood $p_\eta(y)$.
- Requires $\Theta$ to be a measurable subset of a measurable space and $p_\eta(y)$ to be jointly measurable w.r.t. $\eta$ and $y$.
- $\pi$ and $p_\eta$ imply a joint distribution of $\theta$ and $Y$.
- Marginal distribution or predictive distribution of $Y$ is
Updating¶
- Posterior distribution of $\theta$ given $Y=y$:
- All the information in the prior and the data is in the posterior distribution.
- Posterior distribution $\pi_\lambda(d \ell | Y = y)$ of $\lambda[\theta]$ is induced by posterior distribution of $\theta$:
Why use Bayesian methods?¶
- Descriptive : people are Bayesian.
- Normative : people should be Bayesian.
- Practical : "data swamp the prior" so doesn't matter
- My guess: popular because gives a general recipe and smaller error bars than frequentist methods.
- But error bars don't have the same meaning.
Priors¶
- To use Bayesian framework must quantify beliefs and constraints as a prior $\pi$.
- Constraint $\theta \in \Theta$ captured as $\pi(\Theta) = 1$.
- But infinitely many probability distributions assign probability 1 to $\Theta$.
- I've never seen a Bayesian analysis of real data in which the data analyst made a serious attempt to quantify beliefs using a prior.
Priors selected or justified in ~5 ways:
- to make the calculations simple
- because the particular prior is conventional
- so that the prior satisfies some invariance
- with the assertion that the prior is "uninformative" (e.g., Laplace's principle)
- because the prior roughly matches the relative frequencies of values in some population.
Frequentist v. Bayesian¶
Main difference:
Frequentists treat $\theta$ as an unknown element of $\Theta$.
Bayesians treat $\theta$ as if drawn at random from $\Theta$ using $\pi$.
Bayesian approach requires much stronger assumptions.


Summarizing uncertainty¶
Consider Bayesian and frequentist versions of 2 summaries:
mean squared error (frequentist) and posterior mean squared error (Bayesian)
confidence sets (frequentist) and credible regions (Bayesian)
Mean Squared Error and Posterior Mean Squared Error¶
$$ \mbox{MSE}(\widehat{\lambda}(Y), \eta) \equiv E_\eta \| \widehat{\lambda}(Y) - \lambda[\eta] \|^2. $$$$ \mbox{PMSE}(\widehat{\lambda}(y), \pi) \equiv E_\pi \| \widehat{\lambda}(y) - \lambda[\eta] \|^2. $$MSE is an expectation with respect to the distribution of the data $Y$, holding the parameter $\theta = \eta$ fixed.
PMSE is an expectation with respect to the posterior distribution of $\theta$, holding the data $Y = y$ fixed.
Confidence Sets and Credible Regions¶
A random set $I(Y)$ of possible values of $\lambda$ is a $1-\alpha$ confidence set for $\lambda[\theta]$ if $$ P_\eta \{ I(Y) \ni \lambda[\eta] \} \ge 1 - \alpha, \;\; \forall \eta \in \Theta. $$
Probability w.r.t. distribution of the data $Y$, holding $\eta$ fixed.
A set $I(y)$ of possible values of $\lambda$ is a $1-\alpha$ posterior credible region for $\lambda[\theta]$ if $$ P_{\pi( d\theta | Y=y)} (\lambda[\theta] \in I(y)) \equiv \int_{I(y)} \pi_\lambda(d \ell | Y = y) \ge 1-\alpha. $$
Probability w.r.t. marginal posterior distribution of $\lambda[\theta]$, holding the data fixed.
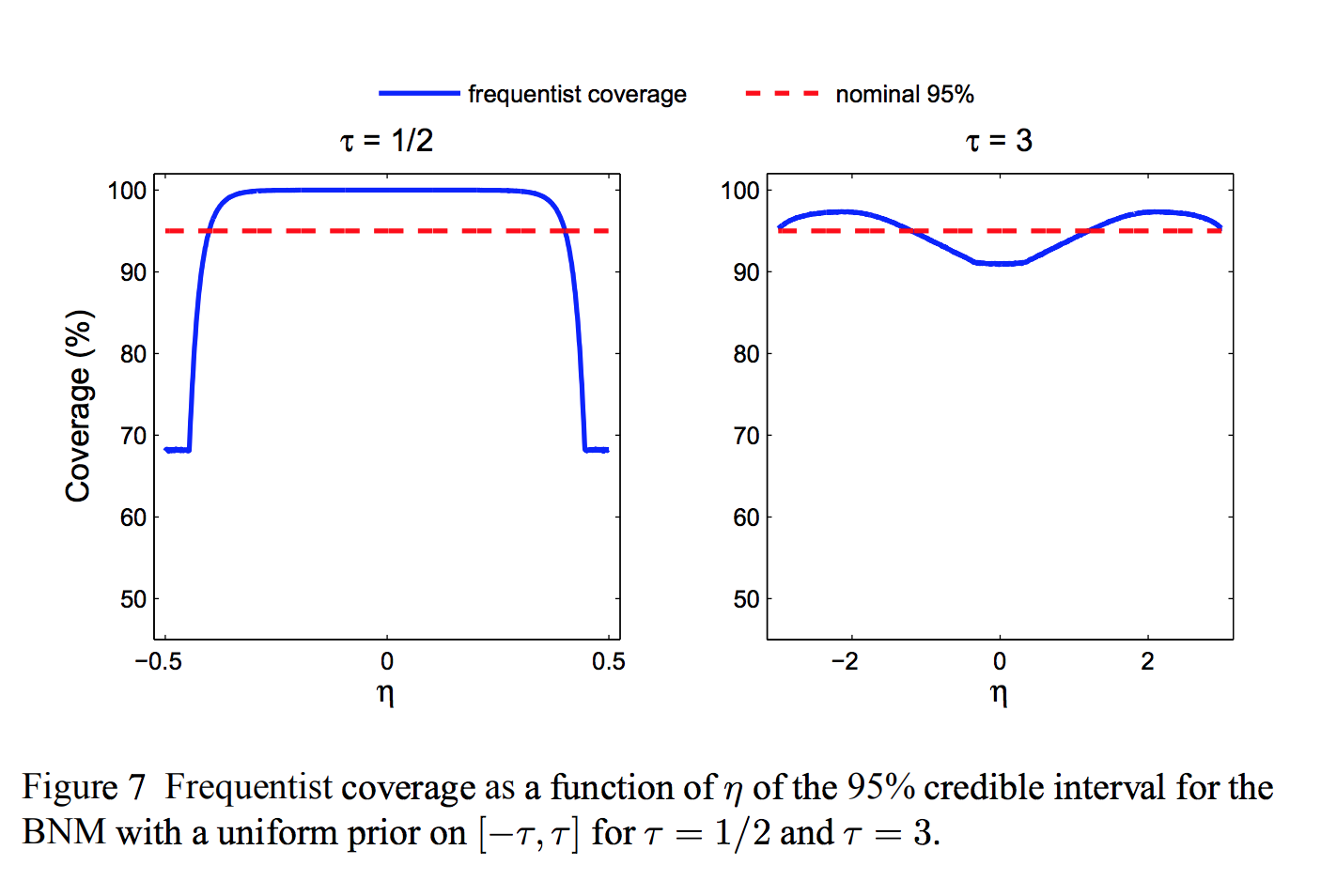
credible level: probability that by drawing from prior, nature generates an element of the set, given the data
confidence level: probability that procedure gives a set that contains the truth
Uncertainties have completely different interpretations¶
Frequentist: hold parameter constant, characterize behavior under repeated measurement
Bayesian: hold measurement constant, characterize behavior under repeatedly drawing parameter at random from the prior
Duality between Bayes and minimax approaches¶
- Formal Bayesian uncertainty can be made as small as desired by choosing prior appropriately.
- Under suitable conditions, the minimax frequentist risk is equal to the Bayes risk for the "least-favorable" prior.
- If Bayes risk is less than minimax risk, prior is artificially reducing the (apparent) uncertainty. Regardless, means something different.
- Least-favorable prior can be approximated numerically even for "black-box" numerical models, a la Schafer & Stark (2009)
Posterior uncertainty measures meaningful only if you believe prior
Changes the subject
Is the truth unknown? Is it a realization of a known probability distribution?
Where does prior come from?
Usually chosen for computational convenience or habit, not "physics"
Priors get their own literature
Eliciting priors deeply problemmatic
Why should I care about your posterior, if I don't share your prior?
How much does prior matter?
Slogan "the data swamp the prior." Theorem has conditions that aren't always met.
- Is all uncertainty random?
Aleatory
- Canonical examples: coin toss, die roll, lotto, roulette
- under some circumstances, behave "as if" random (but not perfectly)
- Epistemic: stuff we don't know


Standard way to combine aleatory variability epistemic uncertainty puts beliefs on a par with an unbiased physical measurement w/ known uncertainty.
Claims by introspection, can estimate without bias, with known accuracy, just as if one's brain were unbiased instrument with known accuracy
Bacon put this to rest, but empirically:
- people are bad at making even rough quantitative estimates
- quantitative estimates are usually biased
- bias can be manipulated by anchoring, priming, etc.
- people are bad at judging weights in their hands: biased by shape & density
- people are bad at judging when something is random
- people are overconfident in their estimates and predictions
- confidence unconnected to actual accuracy.
- anchoring affects entire disciplines (e.g., Millikan, c, Fe in spinach)
what if I don't trust your internal scale, or your assessment of its accuracy?
same observations that are factored in as "data" are also used to form beliefs: the "measurements" made by introspection are not independent of the data
- Can grade Bayesian methods using frequentist criteria
- E.g., what is the coverage probability of a credible region?
Two illustrations¶
Bounded normal mean
Election audits
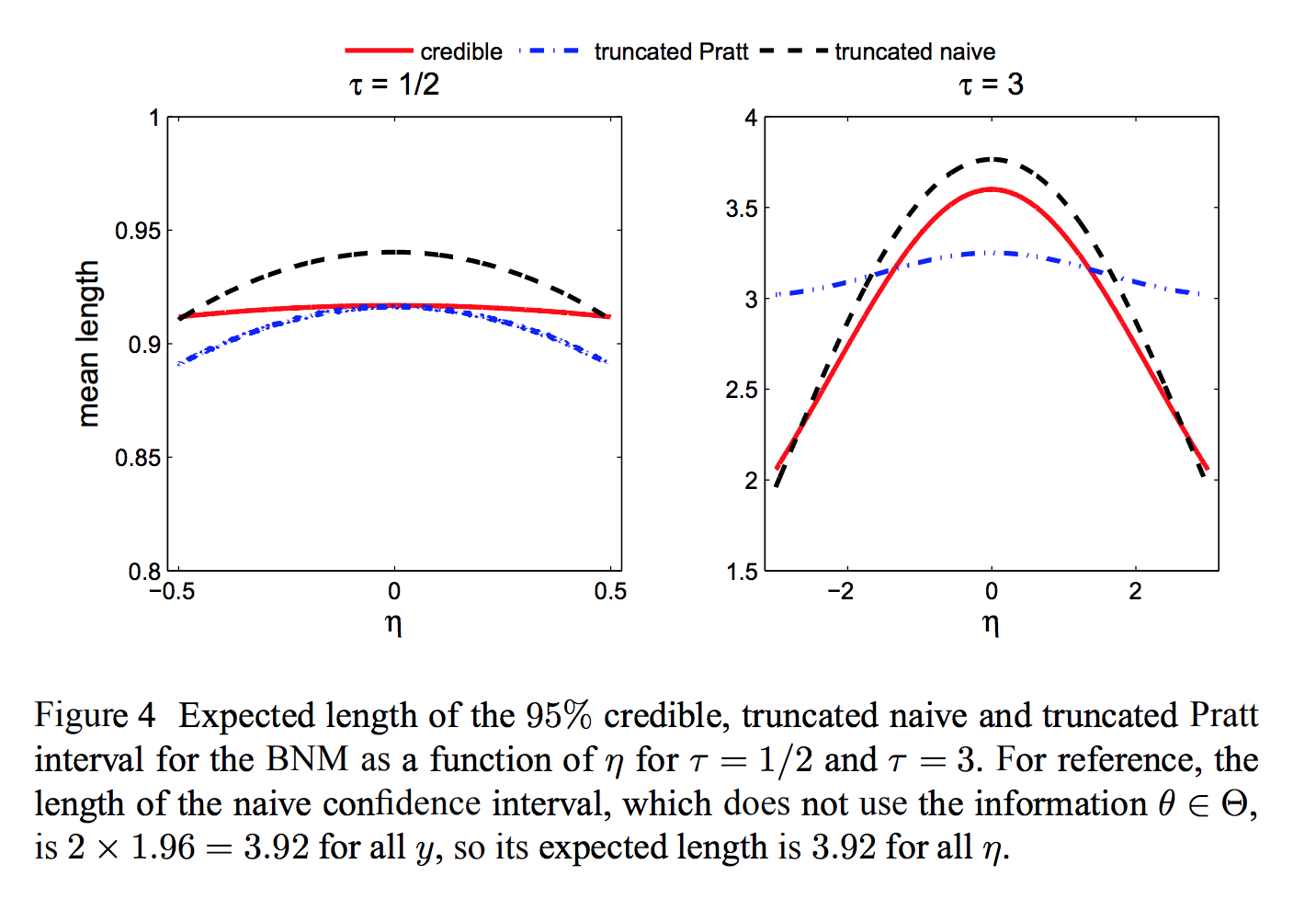
Toy problem: bounded normal mean¶
Observe $Y \sim N(\theta, 1)$.
Know a priori that $\theta \in [-\tau, \tau]$
- Bayes "uninformative" prior: $\theta \sim U[-\tau, \tau]$
Election audits¶
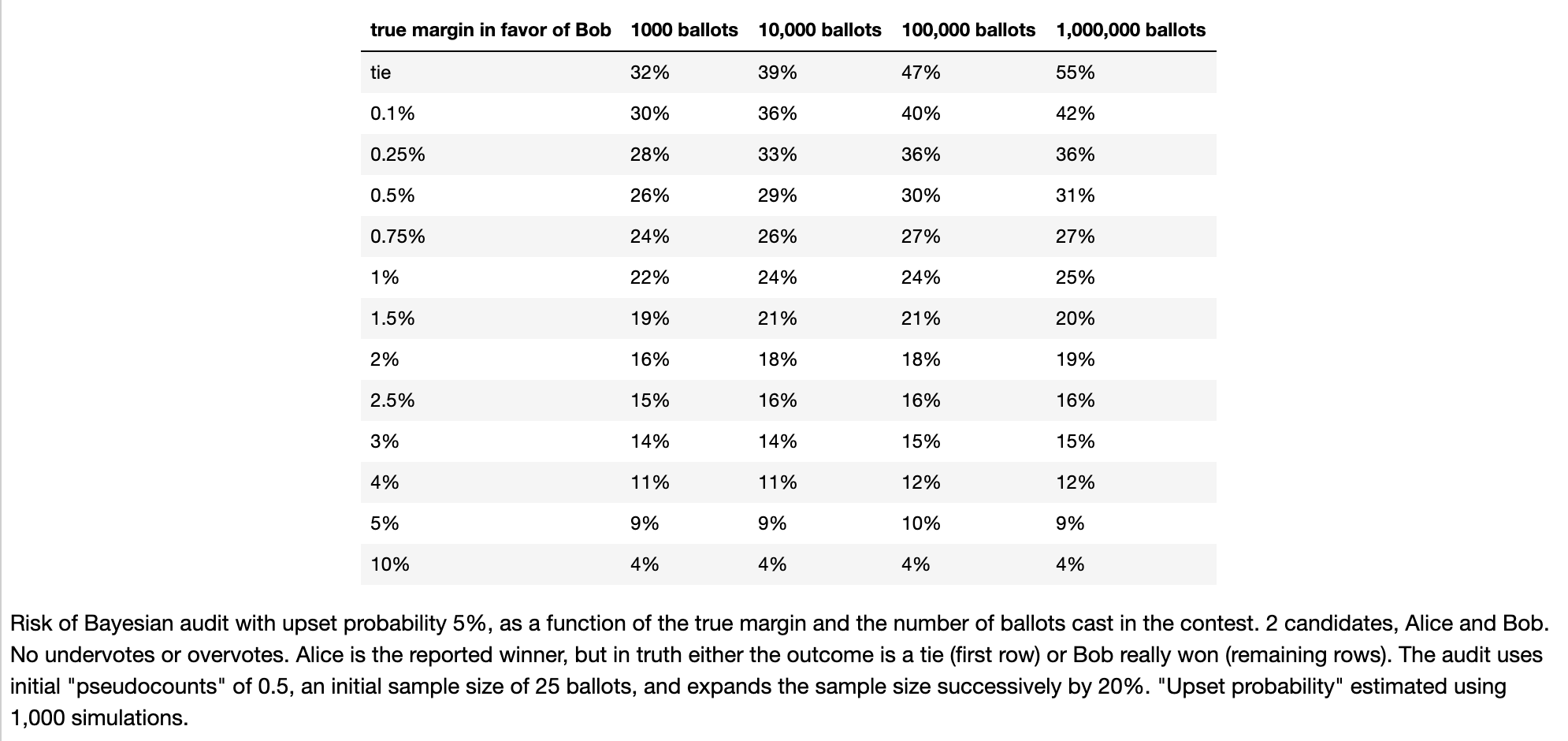
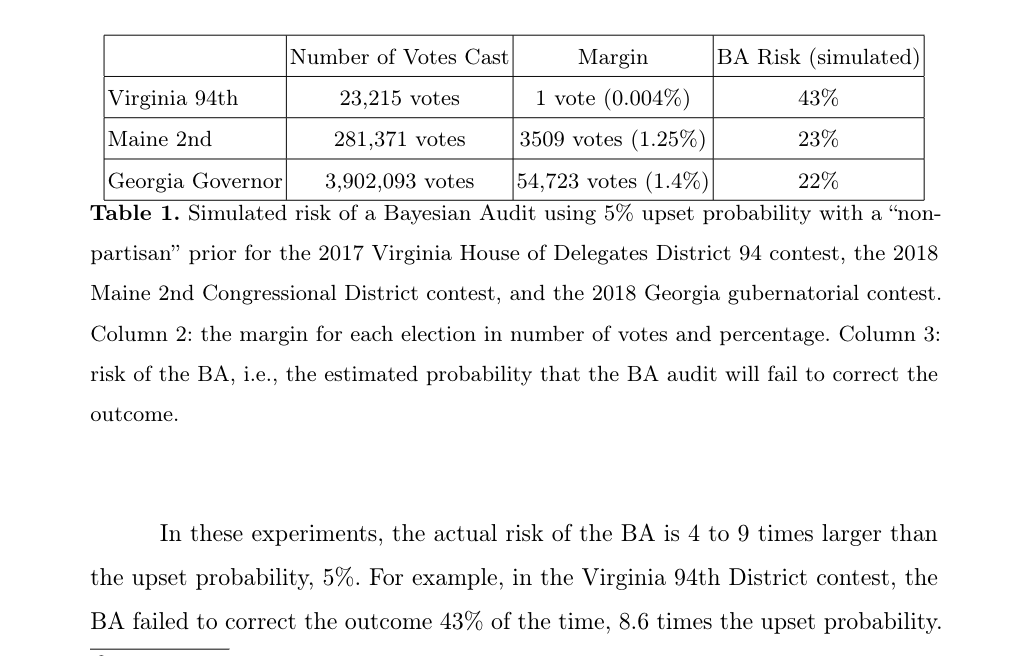
Check whether reported winner(s) really won by looking at random sample of ballots.
Absent convincing evidence that reported winners really won, keep looking.
Risk: probability that the audit does not correct the reported outcome.
Constraint: vote shares are non-negative, sum of shares $\le 1$.
Risk-limiting audit (frequentist)¶
Keep auditing until the (sequential) $P$-value of the hypothesis that the outcome is wrong is sufficiently small.
Known maximum risk, regardless of correct result.
Bayesian audit¶
Keep auditing until the conditional probability that the outcome is wrong, given the data, is sufficiently small.
Requires a prior.
"Nonpartisan" prior is invariant under permutations of the candidate names: "fair."
Includes "flat" or "uninformative" prior.

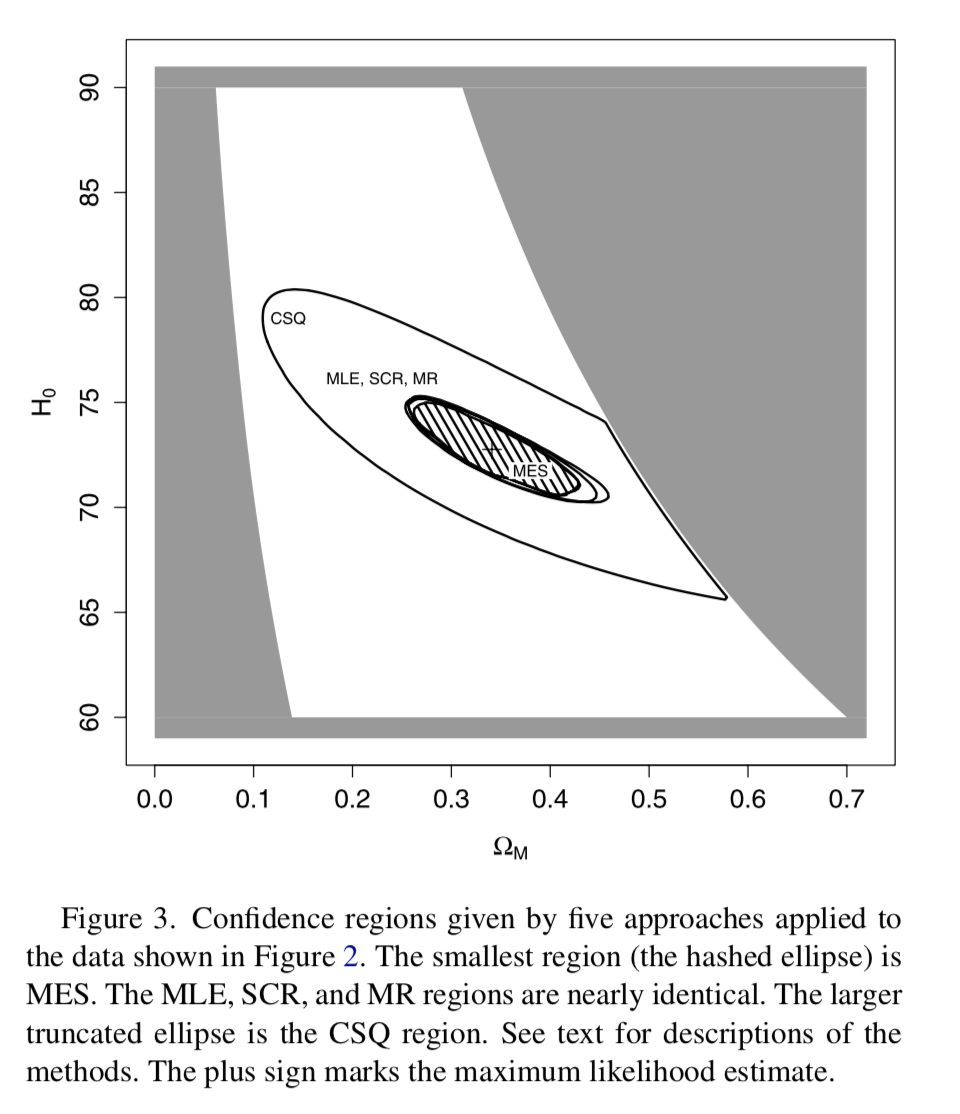
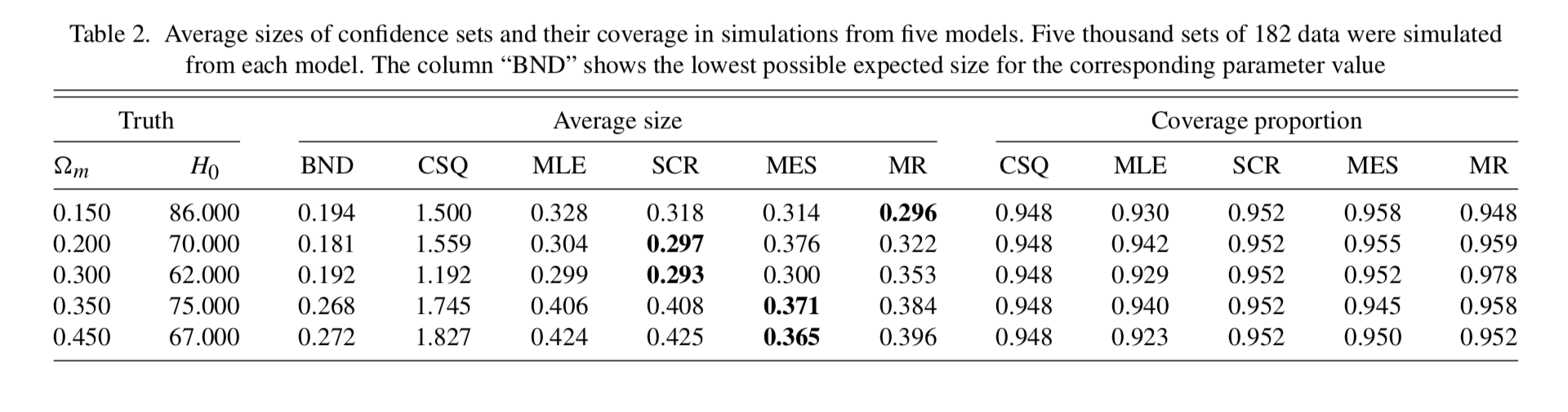
Minimax expected size confidence sets¶
Among all procedures for constructing a valid $1-\alpha$ confidence set for a parameter, which has the smallest worst-case expected size?
Exploit duality between Bayesian and frequentist methods: least-favorable prior.



—George Box
Commonly ignored sources of uncertainty:
Coding errors (ex: Hubble)
Stability of optimization algorithms (ex: GONG)
"upstream" data reduction steps
Quality of PRNGs (RANDU, but still an issue)
References¶
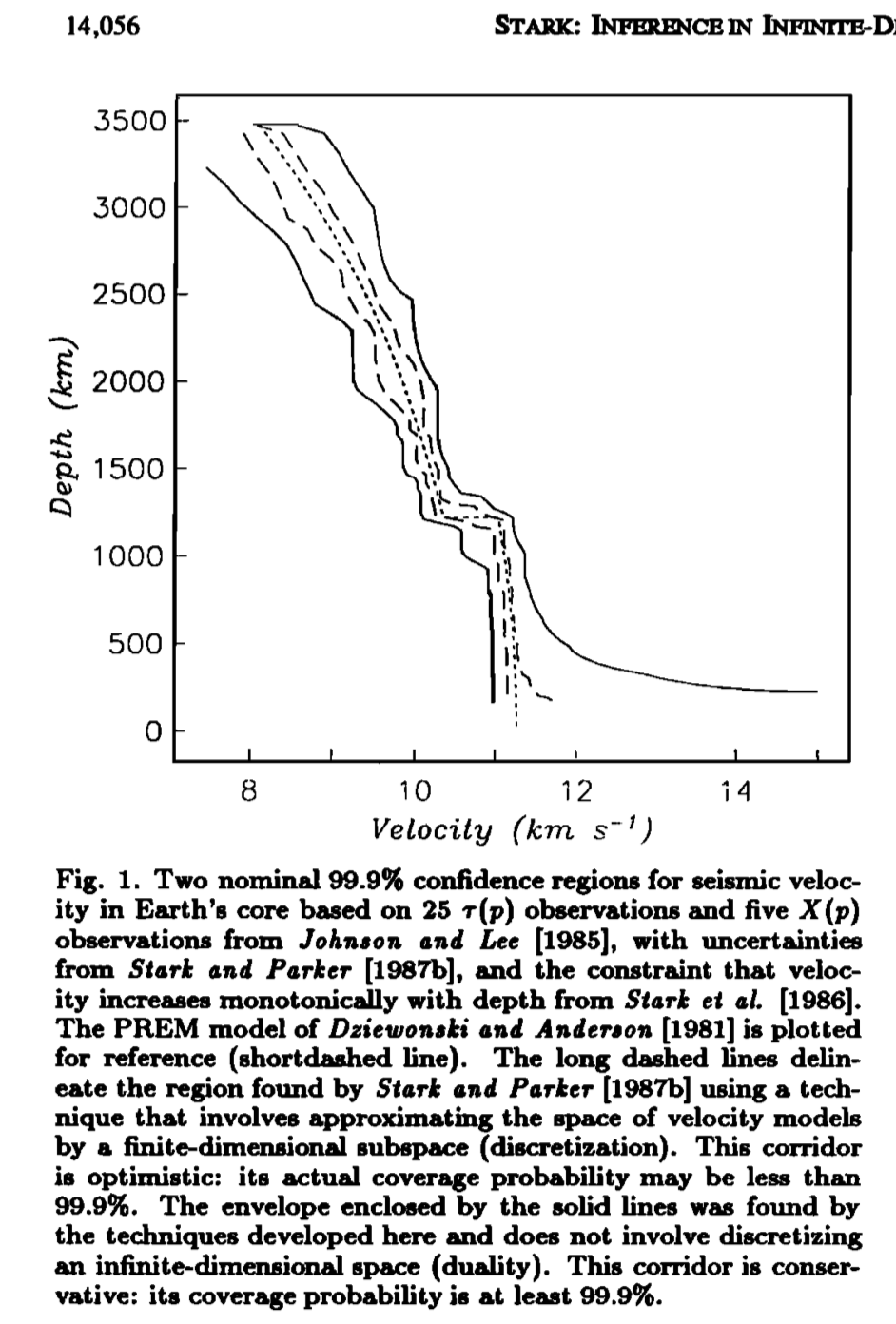
Stark, P.B., R.L. Parker, G. Masters, and J.A. Orcutt, 1986. Strict bounds on seismic velocity in the spherical Earth, Journal of Geophysical Research, 91, 13,892–13,902.
Stark, P.B., 1992. Minimax confidence intervals in geomagnetism, Geophysical Journal International, 108, 329–338. Stark, P.B., 1992. Inference in infinite-dimensional inverse problems: Discretization and duality, Journal of Geophysical Research, 97, 14,055–14,082. Reprint: http://onlinelibrary.wiley.com/doi/10.1029/92JB00739/epdf
Stark, P.B., 1993. Uncertainty of the COBE quadrupole detection, Astrophysical Journal Letters, 408, L73–L76.
Hengartner, N.W. and P.B. Stark, 1995. Finite-sample confidence envelopes for shape-restricted densities, The Annals of Statistics, 23, 525–550.
Genovese, C.R. and P.B. Stark, 1996. Data Reduction and Statistical Consistency in Linear Inverse Problems, Physics of the Earth and Planetary Interiors, 98, 143–162.
Tenorio, L., P.B. Stark, and C.H. Lineweaver, 1999. Bigger uncertainties and the Big Bang, Inverse Problems, 15, 329–341.
Evans, S.N. and P.B. Stark, 2002. Inverse Problems as Statistics, Inverse Problems, 18, R55–R97. Reprint: http://iopscience.iop.org/0266-5611/18/4/201/pdf/0266-5611_18_4_201.pdf
Freedman, D.A., 1995, Some issues in the foundations of Statistics, Foundations of Science, 1, 19–39.
LeCam, L., 1975. A note on metastatistics or 'an essay towards stating a problem in the doctrine of chances', Synthese, 36, 133–160.
Stark, P.B. and D.A. Freedman, 2003. What is the Chance of an Earthquake? in Earthquake Science and Seismic Risk Reduction, F. Mulargia and R.J. Geller, eds., NATO Science Series IV: Earth and Environmental Sciences, v. 32, Kluwer, Dordrecht, The Netherlands, 201–213. Preprint: https://www.stat.berkeley.edu/~stark/Preprints/611.pdf
Evans, S.N., B. Hansen, and P.B. Stark, 2005. Minimax Expected Measure Confidence Sets for Restricted Location Parameters, Bernoulli, 11, 571–590. Also Tech. Rept. 617, Dept. Statistics Univ. Calif Berkeley (May 2002, revised May 2003). Preprint: https://www.stat.berkeley.edu/~stark/Preprints/617.pdf
Stark, P.B., 2008. Generalizing resolution, Inverse Problems, 24, 034014. Reprint: https://www.stat.berkeley.edu/~stark/Preprints/resolution07.pdf
Schafer, C.M., and P.B. Stark, 2009. Constructing Confidence Sets of Optimal Expected Size. Journal of the American Statistical Association, 104, 1080–1089. Reprint: https://www.stat.berkeley.edu/~stark/Preprints/schaferStark09.pdf
Stark, P.B. and L. Tenorio, 2010. A Primer of Frequentist and Bayesian Inference in Inverse Problems. In Large Scale Inverse Problems and Quantification of Uncertainty, Biegler, L., G. Biros, O. Ghattas, M. Heinkenschloss, D. Keyes, B. Mallick, L. Tenorio, B. van Bloemen Waanders and K. Willcox, eds. John Wiley and Sons, NY. Preprint: https://www.stat.berkeley.edu/~stark/Preprints/freqBayes09.pdf
Stark, P.B., 2015. Constraints versus priors. SIAM/ASA Journal on Uncertainty Quantification, 3(1), 586–598. doi:10.1137/130920721, Reprint: http://epubs.siam.org/doi/10.1137/130920721, Preprint: https://www.stat.berkeley.edu/~stark/Preprints/constraintsPriors15.pdf
Stark, P.B., 2016. Pay no attention to the model behind the curtain. https://www.stat.berkeley.edu/~stark/Preprints/eucCurtain15.pdf
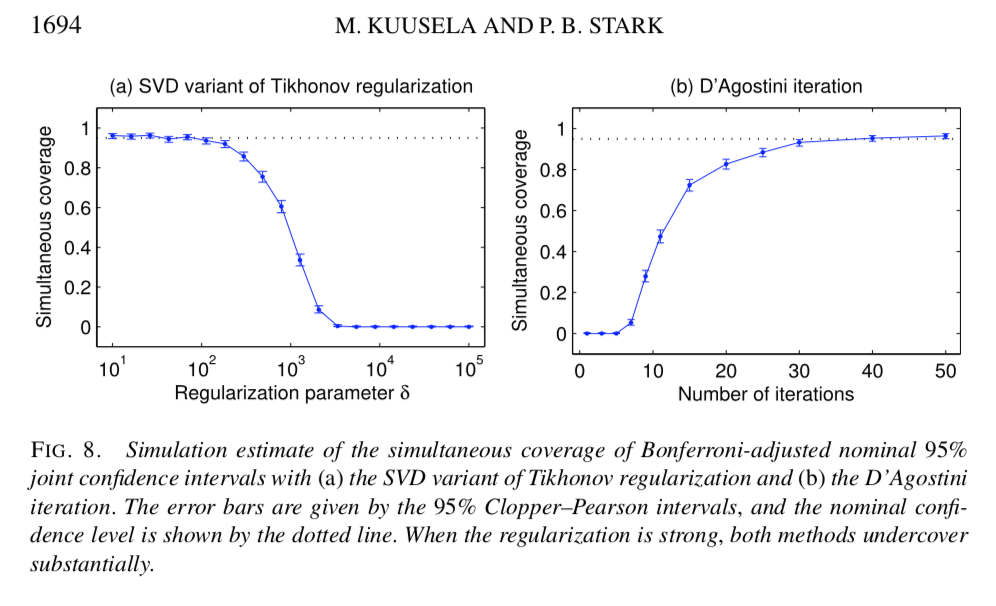
Kuusela, M., and P.B. Stark, 2017. Shape-constrained uncertainty quantification in unfolding steeply falling elementary particle spectra, Annals of Applied Statistics, 11, 1671–1710. Preprint: http://arxiv.org/abs/1512.00905