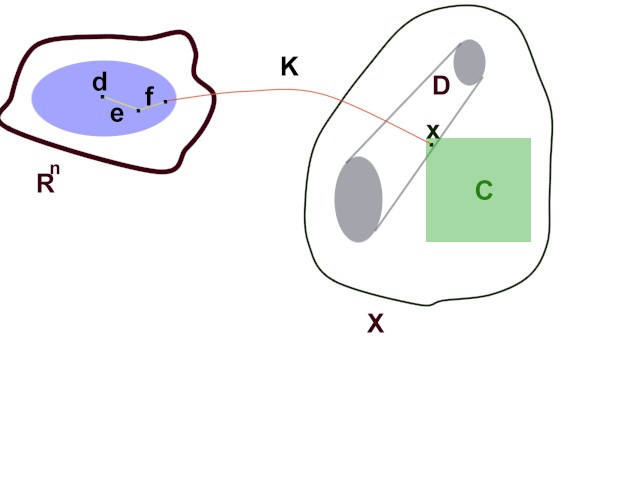
Observe data
d = Kx + e + f
Data vector d is in Rn
x is in C, a known subset of X, an infinite-dimensional linear vector space
K: X --> Rn
is a linear operator.
K might be known only
approximately
e is an n-vector
of stochastic observational errors
assume we know either
i) the joint distribution of the components of e,
or
ii) a set E in Rn
and a number ß,
0 < ß < 1
s.t. P{e is in
E} > 1-ß
f is an n-vector of systematic errors known to be in a subset F of Rn
Seek to learn about x.
For example, we might wish to estimate
x itself
a functional L of x, which might be linear or nonlinear (L: M --> R; x |--> Lx)
Most approaches are based on approximating X by a finite-dimensional subspace M of X.
Very few people worry about the finite-dimensional approximation, but it is absolutely crucial: ignoring it typically grossly understates the uncertainty in the result by arbitrarily large multiples. The apparent uncertainty in finite-dimensional approximations tends to be driven by the approximation, rather than the data.
It has been quite difficult to get across to many physical scientists the message that the uncertainty within the finite parametrization tends to be far too optimistic.
Examples I have worked on include
seismic velocity in Earth's core
topography of the core-mantle boundary
seismic tomography
estimating the geomagnetic field at the core-mantle boundary
earthquake prediction and earthquake aftershocks
helioseismology
microwave cosmology
FTIR Spectroscopy
sparse signal recovery and deconvolution
In some problems, Kx can be computed exactly for all x in C, or at least for all x in the intersection of M and C; in others, the "forward" computation is done approximately (e.g., using finite-element finite-difference techniques, or numerical integration). See the talks by Prof. A.T. Patera and Dr. J.M. Hyman in this workshop for more on estimating the uncertainty in numerical solutions to PDE.
Similarly, sometimes the operator K is not known exactly, for example the domain of integration can itself depend on the data, which are known only with error.
In these approximate cases, it is sometimes possible to bound the error in the forward computation using the fact that x is in C. The bound need not be uniform. (Typically, the bound involves the modulus of continuity of the mapping K restricted to C.)
Stark (1992) gives a fairly general treatment and an example in helioseismology; Backus (1989) treats the case C is an ellipsoid in a Hilbert space X and gives an example in geomagnetism. See also Backus (1996).
Basic idea: seek the estimator  (in some class A of estimators) that does the best, in the worst case (for the worst x in M, the worst f in F, and averaged over the distribution of e).
inf in A supx in C, f in F { El(Âd, Lx)},
for some loss functional l( . , . ). (Typically, the loss is monotone increasing in | Âd - Lx |.) The expectation E is with respect to the distribution of the stochastic error e.
Donoho (1994) establishes a close connection between minimax statistical estimation and optimal deterministic recovery of a linear functional L of a model x in a convex subset C of a Hilbert space X from linear observations Kx+e, when the errors e are Gaussian. In that case, affine estimators turn out to be nearly optimal among all measureable estimators for several common loss functionals l, including absolute and squared error, and the length of fixed-length confidence intervals. For example, a nearly optimal estimator when
l( Âd , Lx ) = | Âd - Lx |2
is of the form
Âd = a + b.d,
with a in R, b in Rn.
This arises from two facts: (i) the difficulty of the full estimation problem can be shown to be that of the hardest one-dimensional subproblem, whose difficulty is intimately related to the modulus of continuity:
w(r; L, K, C) = sup { | Lx - Ly | : || Kx - Ky ||2 <= r and x,y in C }.
(ii) Once the problem is reduced to one dimension, it is a parametric optimization problem: estimating the mean of a normal distribution with unit variance, and mean known to lie in an interval [-t, t]. The near-minimaxity of affine estimators follows from properties of that problem. A current topic of research is optimal variable-length confidence intervals for a bounded normal mean.
Donoho's work was extended to quadratic functionals by Donoho and Nussbaum (1990--yes, the extension appeared before the original result, thanks in part to speedy publishing in statistics).
It does not generally extend to recovery of the entire object x, but Donoho (199?) establishes such a result for sup-norm loss.
See Stark (1992a) for an application of Donoho's approach to a problem in geomagnetism.
The basic idea of "strict bounds" is to find the range of values of some collection of functionals {Lq}q in Q over the intersection of C and the set D of models that satisfy the data "adequately."
Agreement with the data is typically measured in an lp norm. In that case, one often sees
D = { y in X: || Ky - d ||p < t }.
The tolerance t is chosen such that P{ || e ||p < t } > 1-ß. When there are non-ignorable systematic errors f, one can use instead
D = { y in X: inf [ || Ky - d - g||p : g in F ]< t },
with t given as before. In the event the distribution of e is unknown, but it is known that the set E satisfies P{e in E} > 1-ß, one can take
D = { y in X: Ky is in d - E - F }.
The set D is a 1-ß confidence set for x. It is a random set that has probability at least 1-ß of containing the true model x.
Because x is certainly in C, the set CD (C intersect D) is also a 1-ß confidence set for x.

One then seeks for each q in Q
Lq-
= inf { Lqy
: y in CD
} and
Lq+
= sup { Lqy
: y in CD
}.
By construction,
P{ [Lq-, Lq+] contains Lqx for all q in Q } > 1-ß.
That is, the coverage probability of any collection of intervals derived this way is simultaneous, because all the intervals cover whenever CD contains x, an event that has probability at least 1-ß.
Typically, those optimization problems cannot be solved exactly, but for a large class of problems, their values can be bounded above and below by pairs of finite-dimensional optimization problems (exploiting conjugate duality). The results can be purely algebraic (they need not require a topology on X), which is an advantage if the prior physical information does not endow X with a topology. The dual problems are finite-dimensional, but sometimes have infinite-dimensional constraints; those constraints can be imposed conservatively because they involve just the data mapping K, which is known (at least approximately). See Stark (1992b) for details and examples estimating linear functionals and norms for constraint sets C that are cones or ellipsoids.
finite-d approx
lower bound |-------|------|------------------|------|------| upper bound
true range of uncertainty
conservative finite-dimensional
approximation
Somewhat surprisingly, there are problems in which the exact bounds can be found by solving finite-dimensional problems. For example, the problem of finding upper and lower bounds (a confidence envelope) for a probability density function from independent, indentically distributed samples, subject to the prior information that the density has at most k modes, can be solved by a finite number of finite-dimensional linear programs, as can the problem of finding a lower confidence bound for the number of modes of a density. See Hengartner and Stark (1995) for details.
Directions I think hold promise for progress in the next few years include
finding optimal variable-length confidence intervals for linear functionals in linear inverse problems by studying the bounded normal mean problem, then using Donoho's results to apply them to inverse problems in separable Hilbert spaces
exploiting the geometry of the prior information, the measure of misfit, the forward mapping, and the functionals of interest, to sharpen inferences about collections of functionals
treating certain non-convex constraint sets C, such as that arising from sparsity, which is a star-shaped, combinatorial constraint
using the augmented Lagrangian to study problems in which the data mapping K is nonlinear
making one-sided inferences about convex, lower-semicontinuous functionals L (I think this is fairly straightforward)
using interval arithmetic to account for roundoff and numerical precision in the calculation of confidence intervals
Backus, G.E., 1989. Confidence set inference with a prior quadratic bound, Geophys. J., 97, 119-150.
Backus, G.E., 1989. Trimming and procrastination as inversion techniques, Phys. Earth Planet. Inter., 98, 101-142.
Donoho, 1994. Statistical Estimation and Optimal Recovery, Ann. Stat., 22, 238-270.
Donoho, D.L., 199?. Exact Asymptotic Minimax Risk for Sup Norm Loss via Optimal Recovery, Th. Prob. and Rel. Fields
Donoho, D.L. and M. Nussbaum, 1990. Minimax Quadratic Estimation of a Quadratic Functional, J. Complexity, 6, 290-323.
Genovese, C.R., P.B. Stark and M.J. Thompson, 1995. Uncertainties for Two-Dimensional Models of Solar Rotation from Helioseismic Eigenfrequency Splitting, Ap. J., 443, 843-854.
Genovese, C.R. and P.B. Stark, 1996. Data Reduction and Statistical Consistency in Linear Inverse Problems, Phys. Earth Planet. Inter., 98, 143-162.
Hengartner, N.W. and P.B. Stark, 1995. Finite-sample confidence envelopes for shape-restricted densities, Ann. Stat., 23, 525-550.
Pulliam, R.J. and P.B. Stark, 1993. Bumps on the core-mantle boundary: Are they facts or artifacts?, J. Geophys. Res., 98, 1943-1956.
Pulliam, R.J. and P.B. Stark, 1994. Confidence regions for mantle heterogeneity, J. Geophys. Res., 99, 6931-6943.
Stark, P.B., 1992a. Minimax Confidence Intervals in Geomagnetism, Geophys. J. Intl., 108, 329-338.
Stark, P.B., 1992b. Inference in Infinite-Dimensional Inverse Problems: Discretization and Duality, J. Geophys. Res., 97, 14,055-14,082.
Stark, P.B. and N.W. Hengartner, 1993. Reproducing Earth's kernel: Uncertainty of the shape of the core-mantle boundary from PKP and PcP travel-times, J. Geophys. Res., 98,1957-1972.
Stark, P.B., 1993. Uncertainty of the COBE quadrupole detection, Ap. J. Lett., 408, L73-L76.
Stark, P.B., 1995. Reply to Comment by Morelli and Dziewonski, J. Geophys. Res., 100, 15,399-15,402.
©1998, P.B. Stark. All rights reserved.