Spectrum Estimation in Helioseismology

P.B. Stark

Department of Statistics
University of California
Berkeley, CA 94720-3860
www.stat.berkeley.edu/~stark

Presented to the

Department of Statistics
University of California, Los Angeles
7 March 2000

Many figures stolen (with gratitude) from the websites of

• the Global Oscillations Network Group (GONG) and
• the Solar and Heliospheric Observer (SOHO) Solar Oscillations Investigation

For more background information, see those sites, the award-winning Stanford Solar Center, and the 31 May 1996 special issue of Science, devoted to helioseismology and the GONG experiment.

Some of the work described is joint with (variously) I.K. Fodor (LLNL), D.O. Gough (Cambridge), Y. Gu (GONG), R. Komm (GONG), C.R. Genovese (Carnegie-Mellon), T. Sekii (Cambridge), M.J. Thompson (Queen Mary and Westfield College).

Contents

What is Helioseismology?

Helioseismology is the study of the interior of the Sun from observations of the vibrations of its surface.

The Sun is nearly opaque to electromagnetic energy: it takes about 170,000 years for radiation to get to the surface from the core.

On the other hand, the Sun is essentially transparent to neutrinos, and to acoustic waves. Using acoustic energy, we can "see into the Sun" in a way that is quite similar to using ultrasound to image the interior of the human body.

Oscillations of stars have been recognized since the late 1700s. The complicated pattern of the Sun's oscillation was first observed in 1960 by Robert Leighton, Robert Noyes, and George Simon.

The explanation of the pattern in terms of trapped acoustic waves came in 1970-71 by Roger Ulrich, John Leibacher, and Robert Stein. This explanation predicted certain detailed features of the spectrum of solar oscillations that were confirmed by observations made in 1975 by Franz Deubner.

The Sun vibrates constantly in a superposition of acoustic normal modes (like the patterns with which a guitar string vibrates, but for a spherical body rather than a string). The characteristic period of oscillation is about 5 minutes. It takes on the order of a few hours for the energy to travel through the Sun. The velocity amplitude of solar p-modes (modes for which the restoring force is pressure) is about 1 cm/s; the relative brightness variation is about 10^-7.

Mode lifetimes range from hours to months. Modes are typically excited many times per lifetime.

The modes are thought to be excited by turbulence in the convection zone.

About 10⁷ distinct modes are thought to be excited; of those, over 250,000 have been identified, in the sense that their frequencies have been estimated from data. It is thought that within a few years, well over a million modes will have been identified.

Helioseismology is rather like trying to understand how a piano is built from the sounds that it makes when you drop it down a flight of stairs.

Here is a movie of the motion of the surface of the Sun, after filtering out solar rotation. This movie was produced by the GONG group from data recorded by the Cerro Tololo telescope in Chile.

This complicated spatio-temporal pattern of surface motion can be decomposed into modes with different spatial frequencies, oscillating at different temporal frequencies.

To have a wave or a normal mode, the material must "push back" when it is pushed, like a spring. The source of this "restoring force" gives rise to different kinds of oscillations and to modes that sample different parts of the Sun. The observed modes of the Sun are surface gravity modes (f-modes: the f stands for "fundamental") and p-modes, for which the restoring force is pressure.

The particle motion associated with f-modes and p-modes is essentially confined to a region outside the solar core (the ray paths that the energy travels have turning depths above the core), so those modes contain little information about the deepest parts of the Sun.

In the core, negative buoyancy acts as a restoring force, so the core supports "g-modes," for which gravity is the restoring force.

g-modes sample the core well, but their associated particle motion is essentially confined to the core. Their amplitudes at the observable surface of the Sun are quite small, and as yet, there is no convincing report that they have been detected at all.

The modes result from a resonance of traveling waves trapped in the solar interior, which acts as a waveguide for acoustic energy:

Figure from the SOHO-SOI website.

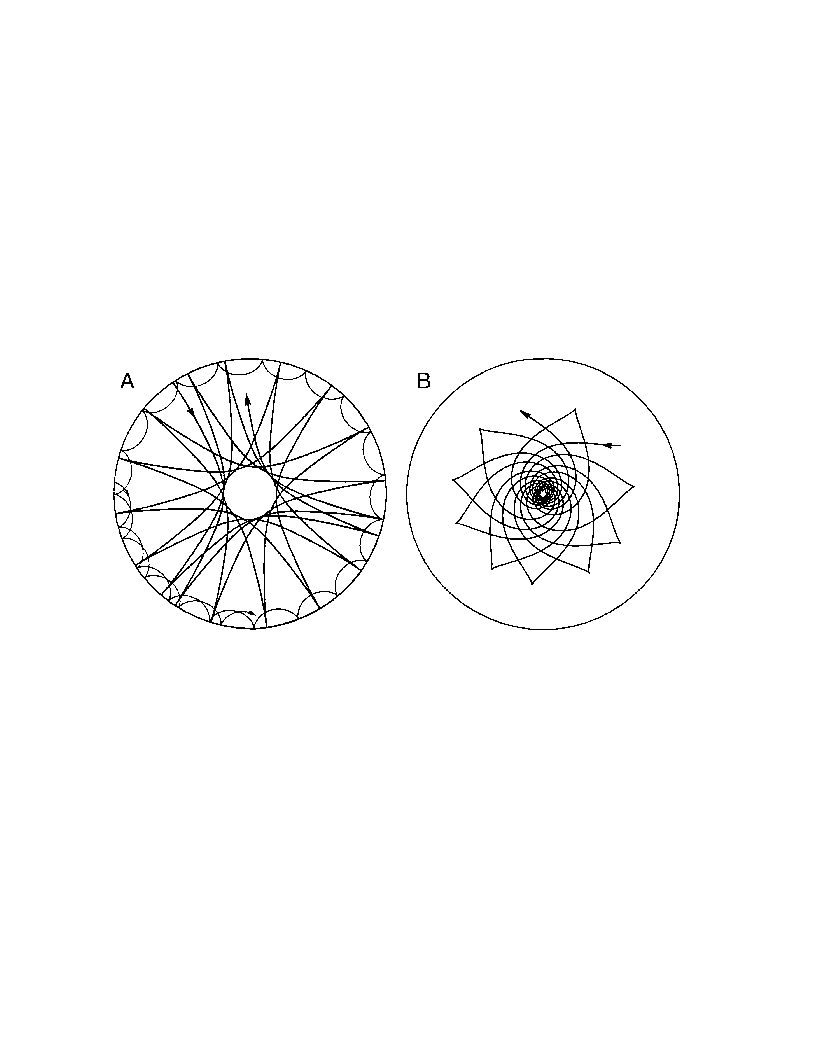
Figure from GONG website. See Gough, Leibacher, Scherrer, and Toomre, Science, 272, 1281-1283. The left figure shows ray paths associated with two p modes (shallow is l=100, n=8; deep is l=2, n=8); the right shows the ray path associated with a g mode (l=5, n=10).

The patterns that individual modes make at the surface of the Sun are quite similar to spherical harmonics Y_lm, which are the analogues of sines and cosines on the sphere. (They are eigenfunctions of Laplaces's equation; they diagonalize any operator that commutes with rigid-body rotation.)

Modes are indexed by 3 "quantum numbers:" the radial order n, the angular degree l, and the angular order m.

The radial order n is the number of nodal surfaces (approximately spheres) with radius.

For each value of l, there are 2l+1 possible values of m: -l, -l+1, ... , 0, 1, ..., l-1, l. The angular degree l is the number of nodal lines on the solar surface, and the difference between l and the absolute value of the angular order m is the number of nodal lines of latitude. For example, when |m| = l, there are no nodal lines of latitude: the modes look like orange segments (sectoral modes).

Here are some views of an l = 20 mode. The first panel has m = l = 20; the second has l = 20, m = 16; the third is a slice through the l = 20, m = 16, n = 11 mode.

Figure from GONG website. See Gough, Leibacher, Scherrer, and Toomre, Science, 272, 1281-1283. Left: line-of-sight component of velocity for l=20, m=20 mode. Middle: line-of-sight component of velocity for l=20, m=16 mode. Right: meridional cut through eigenfunction for density perturbation (scaled for clarity).

Figure from the GONG website.

Modes with small n and l penetrate more deeply into the Sun.

Here is a mathematical idealization of a single mode, with a spatial "frequency" l = 20, m= 16.

Different spatial modes of motion generally have different temporal frequencies of oscillation. Because the modes have different spatial patterns, they sample the solar interior in different ways, and their temporal frequencies allow one to learn about different parts of the Sun.

Here are some filtered, speeded-up sounds of the Sun, processed by A. Kosovichev of the Stanford SOHO-SOI group. 40-day time series of normal mode coefficients were combined and speeded up by a factor of 42,000. One mode (l=1, n=20), three modes, all low-degree modes (l=0, 1, 2, 3).

One can look at the power in the motion as a function of angular scale and temporal frequency, to obtain a multi-dimensional power spectrum:

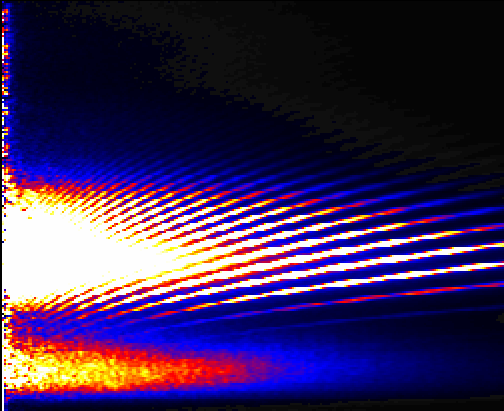
Figure from the GONG website.

The observations of the Sun's oscillations are much better than our observations of Earth's oscillations (low-frequency geoseismology), partly because the oscillations go on constantly (for the Earth, it takes a sizeable earthquake to excite observable oscillations), and partly because we can observe almost half the Sun at any time (on Earth, seismic stations are scattered pretty sparsely). (The "almost" comes from the fact that the solar limb is so noisy that it is usually masked out of the data processing.)

If the Sun were spherically symmetric and did not rotate, the frequencies of the 2l+1 modes with the same values of l and n would be the same.

Rotation and asphericity break the symmetry of the system and the degeneracy of the eigenfrequencies.

Differential rotation splits the "singlets" symmetrically, while asphericity splits them anti-symmetrically.

To first order in the (small) rotation rate, the relationship between the portion of the angular velocity distribution that is symmetric w.r.t. the solar equator, and the odd (in m) component of the splitting, is linear, if one pretends that the eigenfunctions of the oscillations are known.

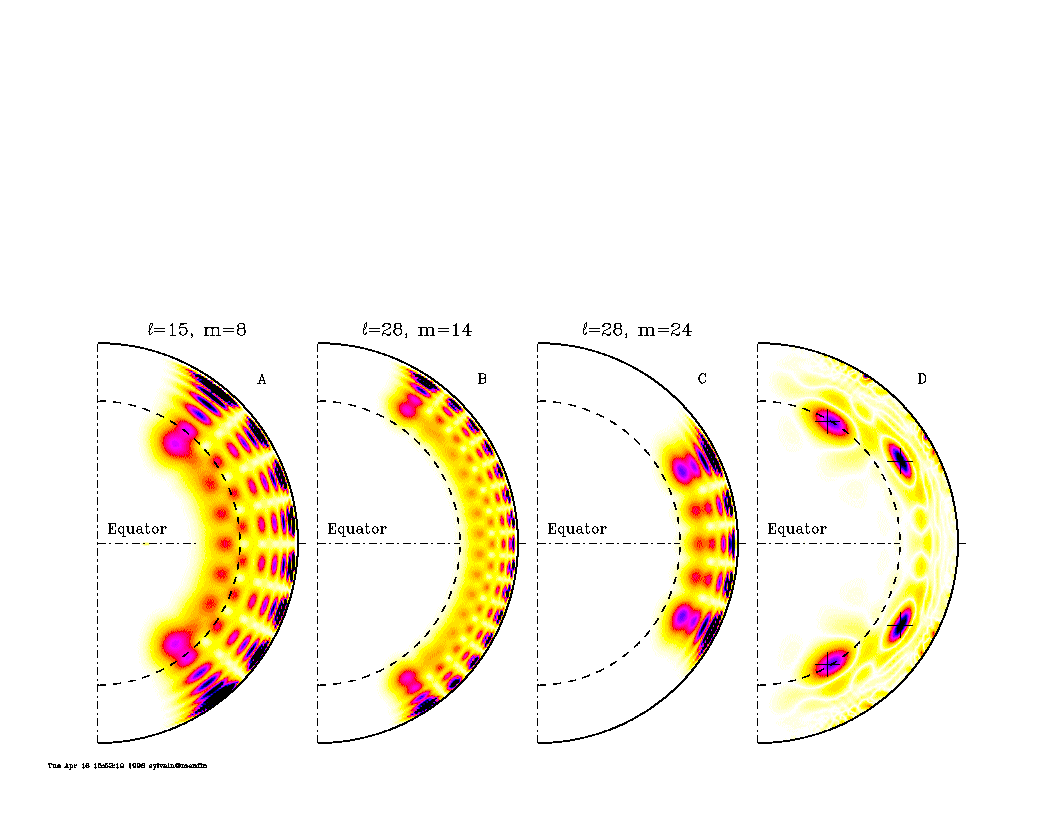
Figure from the GONG website. See Thompson, Toomre, Anderson, and 26 others, 1996. Science, 272, 1300-1305. The left three figures show the sensitivity of some frequency splittings to rotation of the Sun at different latitudes and depths. The rightmost figure shows a combination of splitting sensitivities designed to "target" the rotation at certain places within the Sun.

Overall Goals of Helioseismology

• Learn about the composition, state, and dynamics of the interior of the closest star, including sunspots, the heliodynamo, and the solar cycle

• Test and improve theories of stellar evolution

• Use the Sun as a physics laboratory to study conditions unattainable on Earth (e.g., the neutrino problem, the equation of state, opacity)

Possible By-Products

• Predict space weather by imaging the far side of the Sun

Notable Successes of Helioseismology

The agreement between the predicted spectra for ab initio models and the observed spectra was truly remarkable, but as observations improved (and error bars decreased), it became clear that the "standard solar model" was wrong in important ways.

Revised depth of the solar convection zone.

Douglas Gough showed that the convection zone was probably substantially thicker than previously thought.

Falsification of dynamo models with rotation constant on cylinders

Since the mid-1980s, many studies of solar rotation using frequency splittings have shed doubt on dynamo models that required rotation to be roughly constant on cylinders in the convection zone.

Errors in opacity calculations of numerical nuclear physicists

The "standard solar model" fit the estimates of soundspeed better if the opacity at the base of the convection zone was modified in an ad hoc way. Checking with the physicists who produced the original opacity figures led to the discovery that the bound-state contribution of iron had been underestimated, as a result of the hydrogenic approximation. That error led to a 10%-20% error in the opacity at the base of the convection zone. Revised opacity calculations brought theory in line with solar observations, and explained the pulsation period ratios of Cepheid stars, previously a mystery.

Progress in the solar neutrino problem.

Measurements of the solar neutrino flux over 25 years lower than predicted by nuclear physics in conjunction with stellar evolutionary models. Not yet clear whether the problem is with nuclear physics (e.g., neutrinos might have mass) or with the theory of stellar evolution. Observations of the modes that do probe the core (to some extent) make low Helium abundance in the core an implausible explanation of the solar neutrino deficit.

 

Recent Announcements

"Plasma rivers" in the Sun. The SOHO-SOI/MDI team announced last year the discovery of "plasma rivers" in the Sun, (press release) where the flow of solar plasma is about 10% faster than the surrounding material. This was one of the top 10 NASA stories for 1997.

Figures from Stanford Univ., the SOHO-SOI/MDI website.

Here is a movie produced by the SOHO team showing waves generated by a solar flare.

Two Current Helioseismic Experiments

There are a number of experiments in different countries, ranging from networks that view the Sun as a star (spatially unresolved) to very high resolution single stations. I'll just describe the two I am affiliated with. These are the experiments with high spatial resolution and the highest duty cycles. Duty cycle is quite important, because gaps in the observation series result in spurious artifacts in the estimates of the spectrum of solar oscillations.

The Global Oscillations Network Group (GONG) is a 6-station ground-based network funded by the NSF.

The Solar and Heliospheric Observer Solar Oscillations Investigation (SOHO-SOI) is a satellite-based experiment funded by NASA and ESA.

Both try to get essentially continuous observations, GONG, by having a globe-spanning network on which the Sun never sets, and SOHO-SOI by observing from space (a halo orbit around the L1 Lagrange point).

Figure from the GONG website

These cubes are the heart of the Michelson Doppler Interferometers used both by GONG and SOHO-SOI/MDI to determine the pattern of motion of the solar surface. Fourier tachymeters for measuring solar oscillations were first developed by Tim Brown (HAO/NCAR) in the 1980's. The basic idea is to use a sequence of filters to isolate an absorption line originating in the mid-photosphere (Ni I, 676.8nm), then use tunable interferometers to measure the intensity at several frequencies in a small band; these can in turn be converted to estimates of the Doppler shift in the absorption line, and hence to a velocity. This is done in each pixel of the image (in a CCD camera essentially identical to ones used in video cameras), resulting in a spatially resolved image of the velocity of the Sun's surface. Both GONG and SOHO-SOI/MDI produce one such image per minute. The SOHO-SOI/MDI camera has 1024 by 1024 pixels; the GONG cameras have 242 by 256 pixels. The overall data collection rate for GONG is about 38Gb/month. The basic analysis unit for studying oscillations is a time series of 36 or 72 days of such time series (51,840 or 103,680 images).

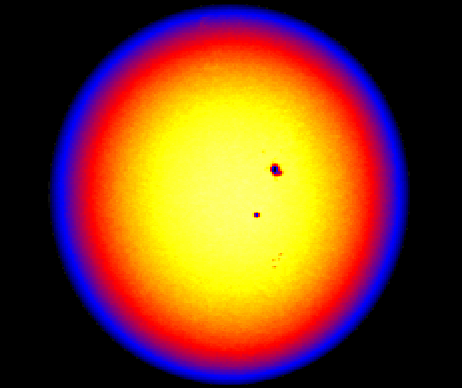
Figure from the GONG website

This is a raw intensity image of the Sun through the GONG instrument.

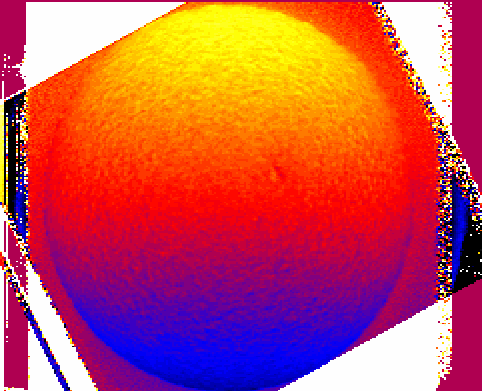
Figure from the GONG website

This is an image of the velocity inferred from the Doppler measurements. Top-bottom should be East-West; the gradient from red to blue is the signature of the Sun's rotation.

Figure from the GONG website

This is a velocity image after filtering to remove the Sun's rotation.

The GONG Data Pipeline

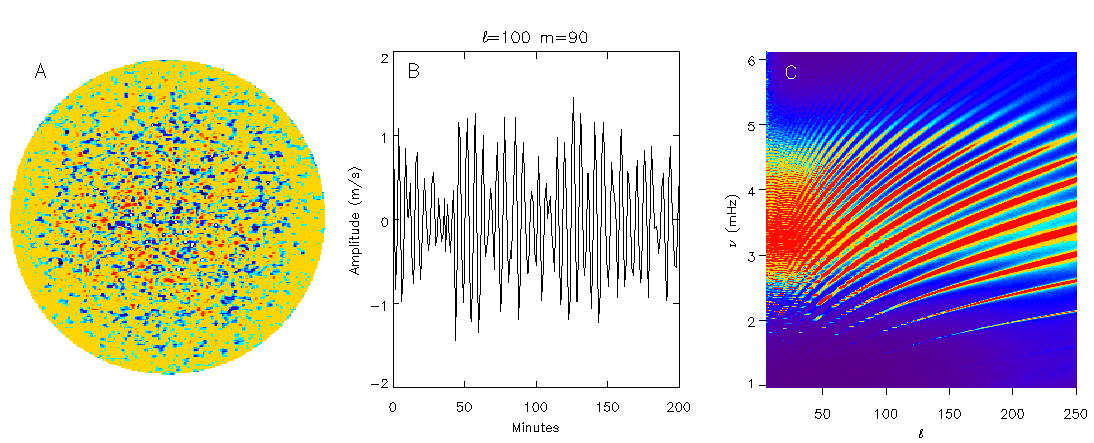Figure from the GONG website. See Harvey, Hill, Hubbard, and 14 others, 1996, Science, 272, 1284-1286. Schematic of the data processing flow: time series of images like that on the left are each decomposed into spherical harmonics, giving many time series of spherical harmonics like that in the middle. The spectrum of each of those time series is estimated, as a function of frequency. The acoustic power as a function of the frequency and angular wavenumber can then be estimated, as on the right.

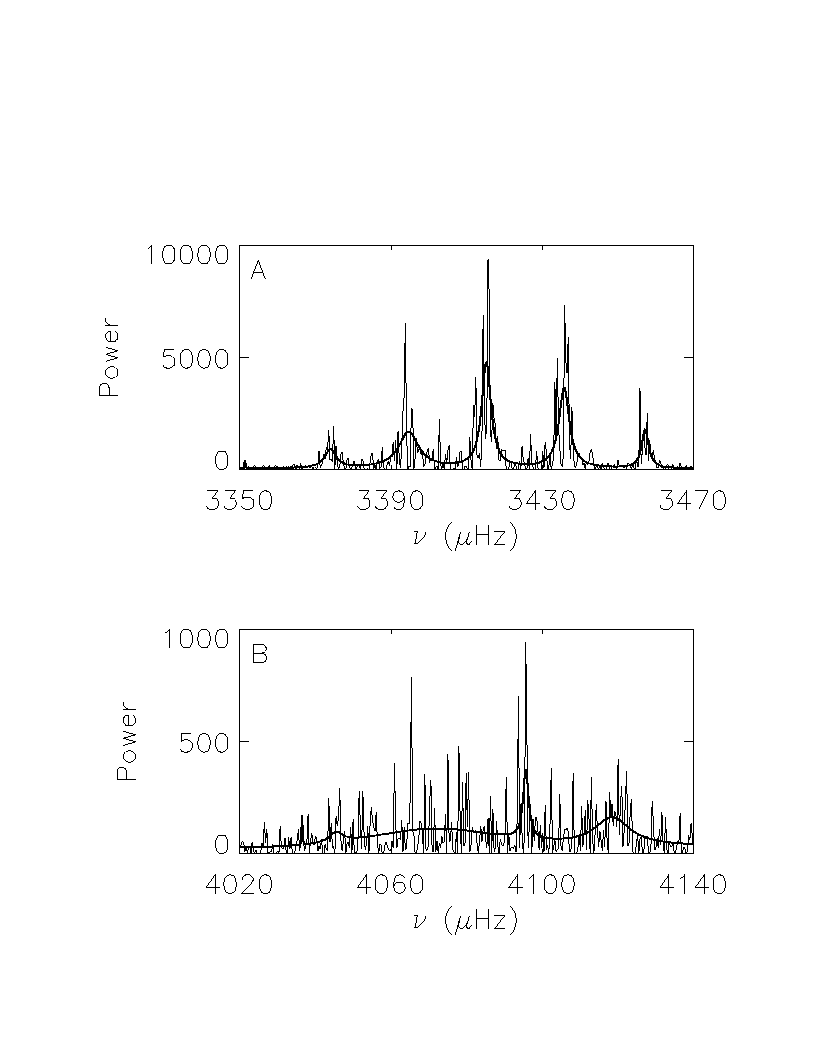
From GONG website. See Hill, Stark, Stebbins, and 23 others, 1996. Science, 272, 1292-1295. Examples of spectra well and poorly fitted by the parametric models used to estimate the frequency, amplitude, linewidth, and background power of solar modes.

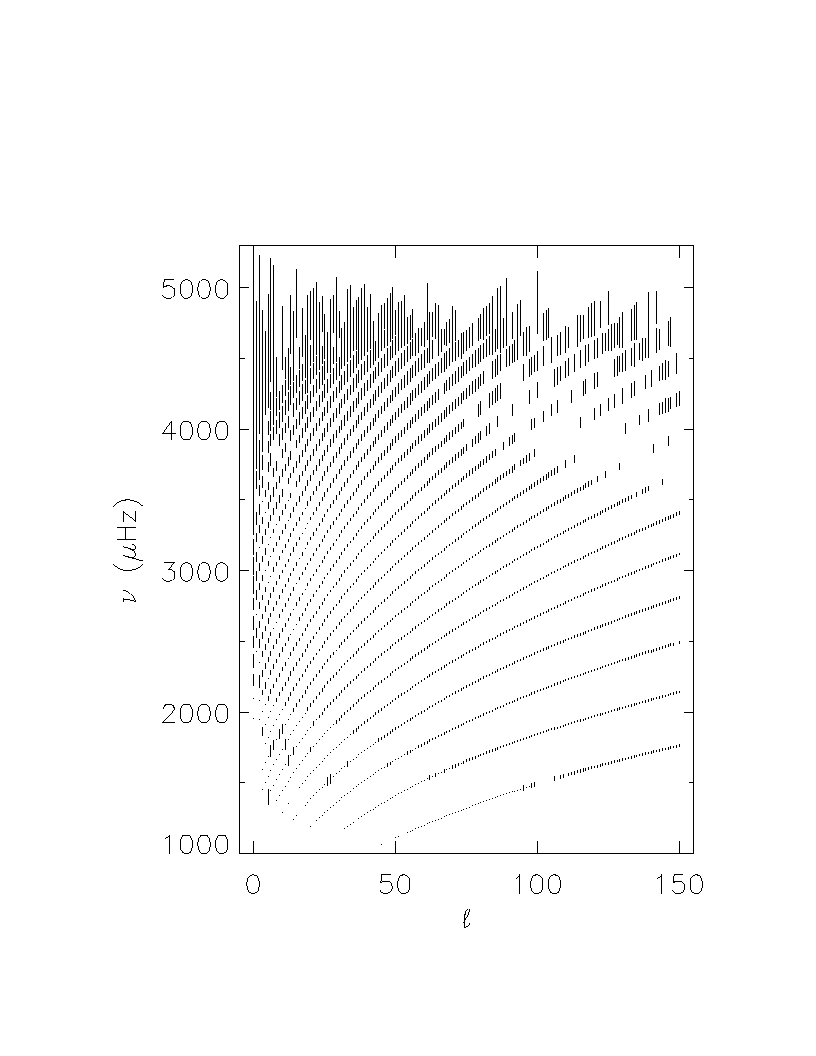
Figure from the GONG website. See Hill, Stark, Stebbins, and 23 others, 1996. Science, 272, 1292-1295. Central frequencies of modes as a function of l, averaged over m, with formal error bars magnified by 200.

Major Processing steps in the GONG Pipeline

1. Read tapes from sites.
2. Correct images for CCD characteristics (dark and clamp)
3. Transform intensities to Doppler velocities.
4. Calibrate velocities using daily calibration images^*
5. Determine image geometry and modulation transfer function (from atmospheric effects, lens cleanliness, instrumental characteristics, etc.^*
6. High-pass filtering to remove steady flows.
7. Remap images to heliographic coordinates, resample evenly in longitude and latitude using bicubic interpolation, correct for line-of-sight^*
8. Transform to spherical harmonics: apply spatial window in heliographic coordinates, Legendre stack in latitude, FFT in longitude^*.
9. Adjust the spherical harmonic amplitudes for the estimated modulation transfer function
10. Merge time series of spherical harmonic coefficients from different stations, using weights to account for relative uncertainties^*
11. Fill data gaps of up to 30 minutes by autoregressive/moving average (ARMA) modeling^*.
12. Take periodogram of the time series of spherical harmonic coefficients^*.
13. Fit parametric model (Lorentzians plus background) to peaks in the power spectrum by iterative approximate maximum likelihood^*.
14. Identify quantum numbers of the modes, report frequencies, linewidths, background power, and uncertainties^*.

Asterisks (^*) indicate steps that could be improved or possibly eliminated by better statistical methodology.

Inversion

The two principal kinds of information one can extract from helioseismic data are spatial averages of the speed with which seismic waves travel in the Sun, and spatial averages of the speed with which parts of the Sun are moving relative to other parts (because the seismic waves are advected with the material). Until a few years ago, the features studied were global, and the studies were based on normal mode frequency estimates; more recently, scientists have started using "local area helioseismology" to image local features of the Sun, such as the flow beneath sunspots, using time series of images more directly.

These inference (inverse) problems are quite difficult, but they share mathematical and statistical structure with inverse problems in may fields, including geophysics and medical imaging.

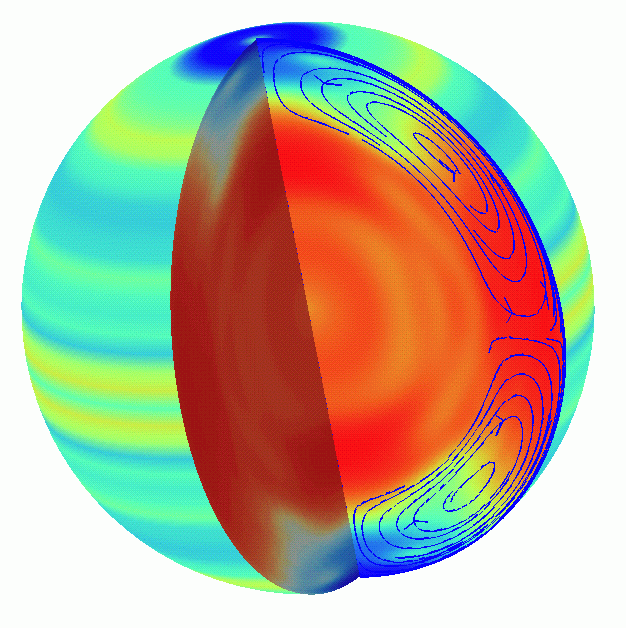
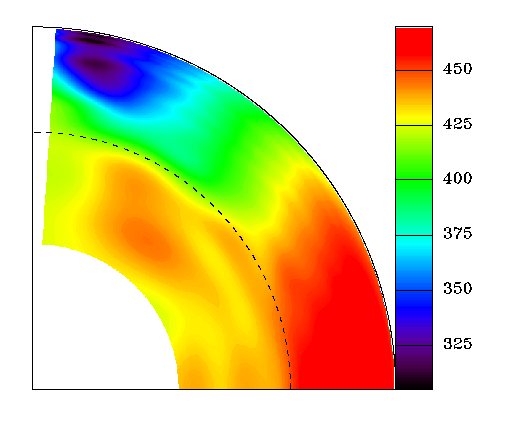
Figure from the GONG website. See Thompson, Toomre, Anderson, and 26 others, 1996. Science, 272, 1300-1305. Left panel is an estimate of the average rotation as a function of latitude and radius using an approximate separation of latitude and radius in the forward problem. Right panel is a regularized least-squares model in a tensor-product basis, with second-derivative smoothing and an arbitrary choice of Lagrange multiplier.

Figure from the GONG website. See Thompson, Toomre, Anderson, and 26 others, 1996. Science, 272, 1300-1305. Sections through the two-dimensional images above, at three latitudes. Shading is ±1SD(nominal).

Statistical Questions and Opportunities

Data Reduction and Calibration: how best to account for instrumental drifts, changes in lens cleanliness, etc.

Signal processing and spatial spectrum estimation.

Temporal spectrum estimation.

Parameteric spectrum fitting.

Inverse problems: nonparametric regression with indirect observations, imprecisely known forward operators, multidimensional regression functions; regularization and inference; unknown noise levels; plug-in bias estimates;...

Techniques being developed or adapted and applied

Here are examples of some of the areas I'm familiar with in which new techniques are being developed and applied.

Spectrum estimation:

Spherical wavelet transformations for image denoising (Tenorio)

Multitaper spherical spectrum estimation, accounting for masking and noise (Schafer, Stark)

Minimum l₁ spectrum estimation (Genovese, C. and P.B. Stark, 1993. l₁ spectral estimation: Algorithms and tests of super-resolution, in GONG 1992: Seismic Investigations of the Sun and Stars, Proc. Astr. Soc. Pac. Conf. Ser., 42, T. Brown, ed., 453-456.)

Gap-aware multitaper temporal spectrum estimates, and uncertainties for multitaper spectra via resampling (Fodor, I. and P.B. Stark, 1999. Multitaper Spectrum Estimation for Time Series with Gaps, submitted to IEEE Trans. Signal Processing.)

Wavelet shrinkage denoising of temporal power spectra (Komm, R., Y. Gu, P.B. Stark, and I. Fodor, 1999. Multitaper Spectral Analysis and Wavelet Denoising Applied to Helioseismic Data, Astrophysical J., 519, 407-421.)

Adaptive model selection in estimating spectral parameters (Korzennik, Stark)

Combining cross-branch information using resampling (Korzennik, Stark)

Nonparametric tests of solar-cycle changes in free oscillation frequencies (Gough, D.O. and P.B. Stark, 1993. Are the 1986-1988 changes in solar free-oscillation frequency splitting significant?, Ap. J., 415, 376-382.)

Inversion:

Minimax error estimates for rotation inversions incorporating prior physical constraints (Genovese, C.R., P.B. Stark and M.J. Thompson, 1995. Uncertainties for Two-Dimensional Models of Solar Rotation from Helioseismic Eigenfrequency Splitting, Ap. J., 443, 843-854)

A posteriori estimates of the bias in regularized least-squares models (Genovese)

Multiple comparison procedures tailored to infer spatial variations in solar properties (Brown, Gough, Stark)

Construction of localized averages optimized for testing specific hypotheses (Gough, D.O., T. Sekii, and P.B. Stark, 1996. Inferring spatial variation of solar properties from helioseismic data, Ap. J., 459, 779-791)

Nonparametric tests for the independence of excitation of different modes from combined time series (Gough, Stark)

Accounting for forward model mis-specification in assessing the uncertainty in images (Stark, P.B., 1992. Inference in infinite-dimensional inverse problems: Discretization and duality, J. Geophys. Res., 97, 14,055-14,082.)

Developing optimal estimators for linear functionals of restricted infinite-dimensional parameters (Stark)

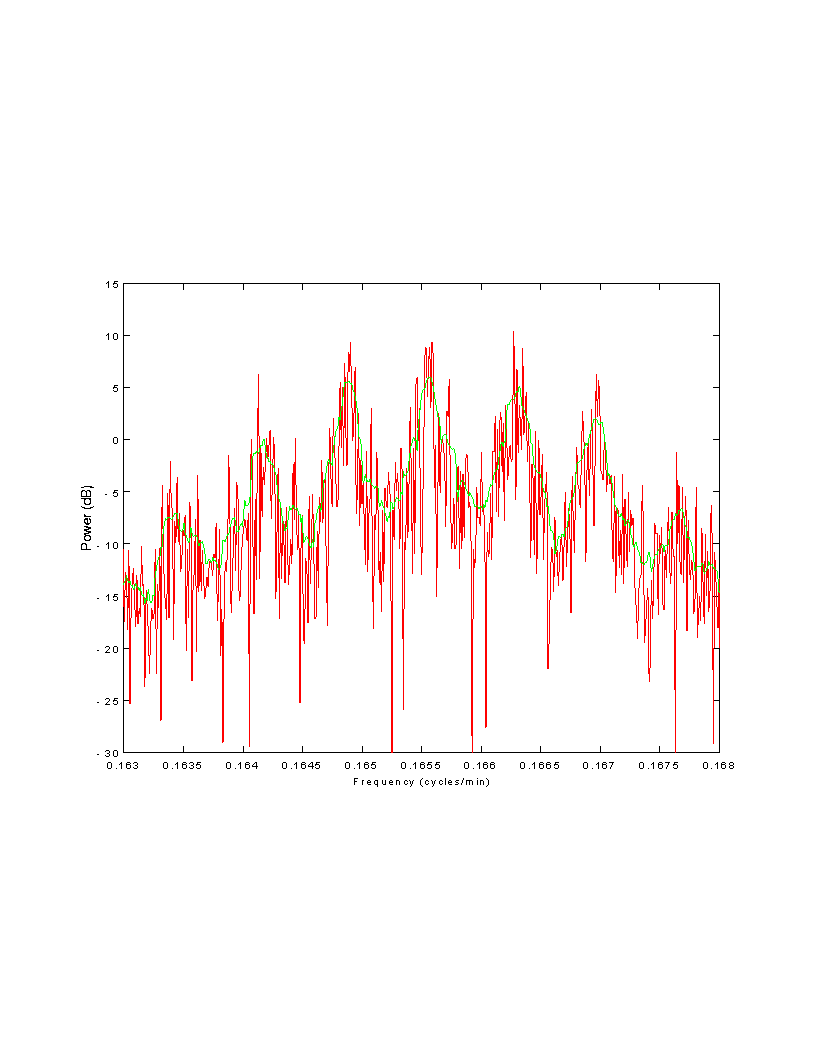
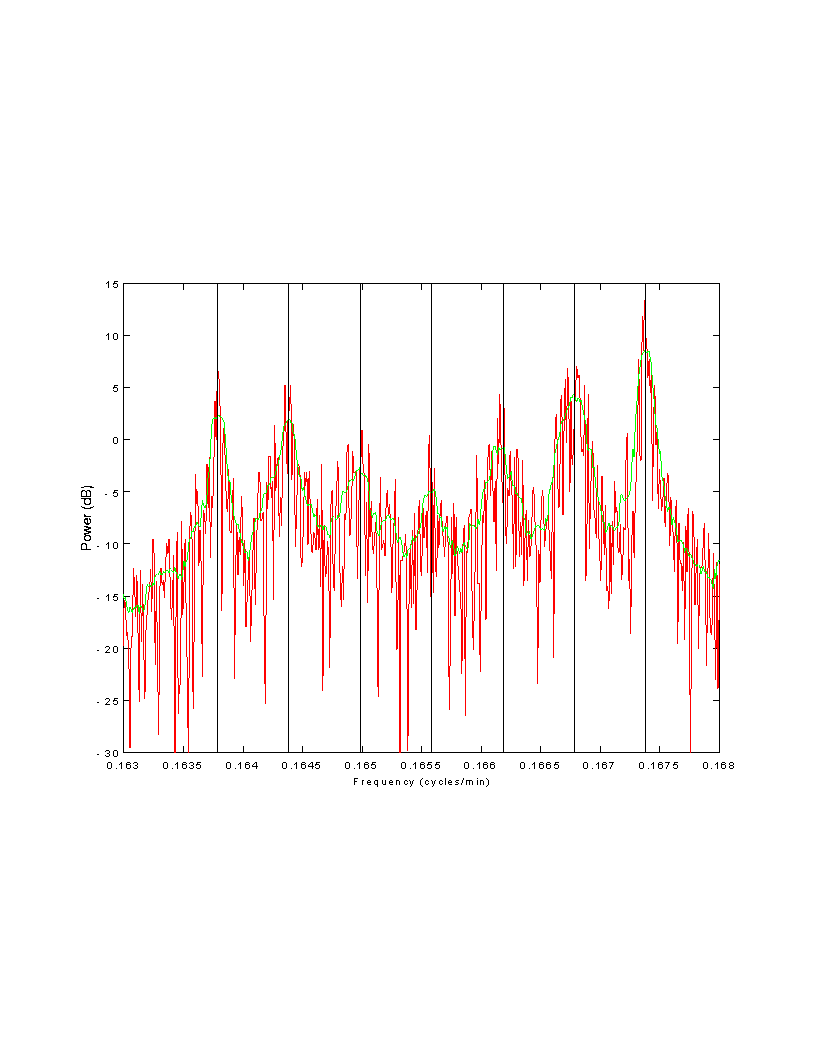
Periodogram (red) and gap-aware multitaper (green) estimates from synthetic data, 25 modes.