The Hypercube Revealed

The best place to start exploring 4-dimensional space is with the hypercube (or 4-cube, tesseract, octachoron). And the best way to understand the hypercube is by analogy with its 3-dimensional version, the 3-cube.

The viewer shows a 4-cube by default. We'll also use it to show a 3-cube and draw parallels between the two. (You can follow on two viewers by opening the viewer page in two browser windows; to display a 3-cube, click polytopes..., then in the polytopes dialog select dimension 3 and click OK). In both windows, click reset polytope and make sure w-perspective and z-perspective are unchecked. Both viewers should show:

cube initial view, 3-d and 4-d

In n dimensions, an n-cube's edges run in n perpendicular directions. For each cube in its initial position, the first direction, x, is horizontal, the second, y, is vertical, and the rest are perpendicular to the plane of the screen, so without perspective they are hidden. Rotating each cube slightly in the xy-plane by pressing the xy button gives something like this (to reverse rotate, right- or Ctrl-click):

xy-rotated cube, 3-d and 4-d

Since the rotation only involves x and y, the edges perpendicular to the screen remain so, still hidden. Now press xz to rotate each cube horizontally, getting something like this:

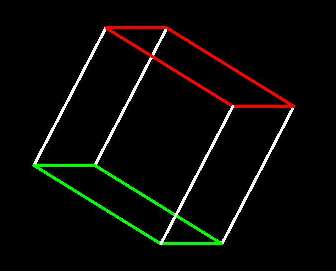
after xz-rotation, 3-d and 4-d

Now edges are seen running in three directions. For the actual cube edges, these directions are all perpendicular, but since the screen is two-dimensional, their projections cannot be. After the xz-rotation, the edges that were formerly aligned in the z direction now have an "x component" and are seen on the screen as horizontal.

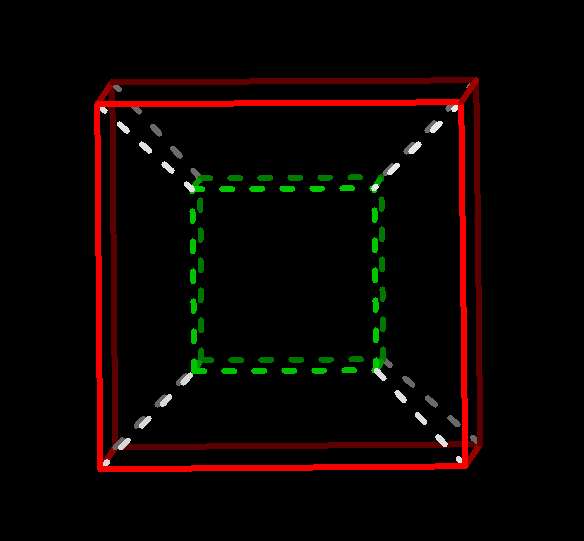
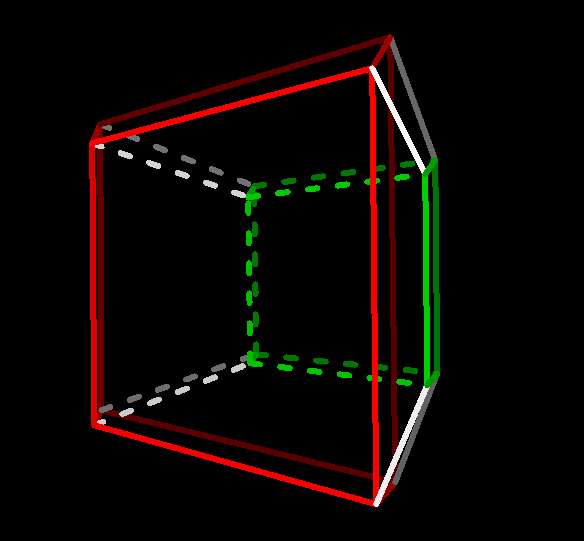
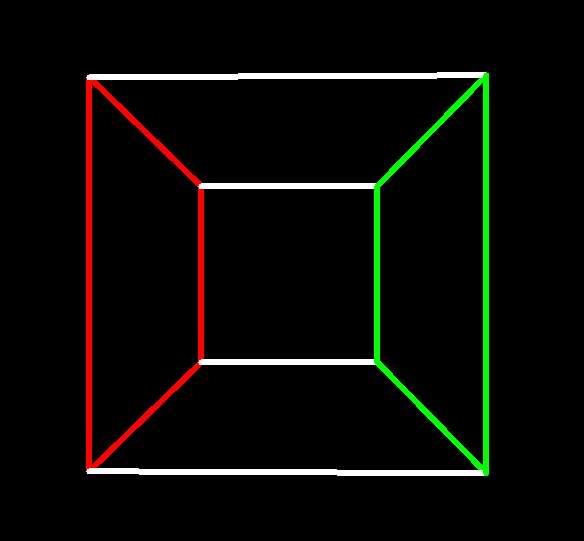
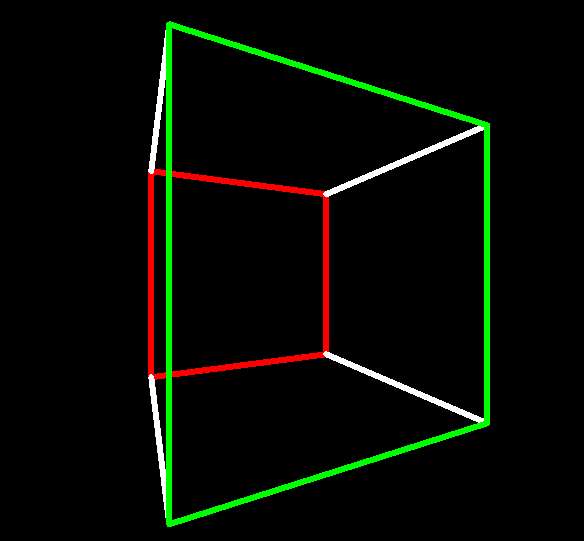
Notice that the 3-cube can be seen as the two squares that were previously superimposed now displaced and with corresponding corners (vertices) joined:

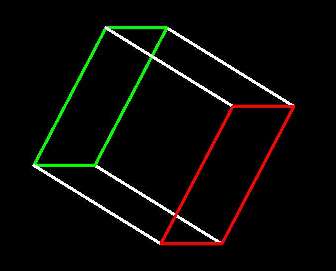
opposite faces of 3-cube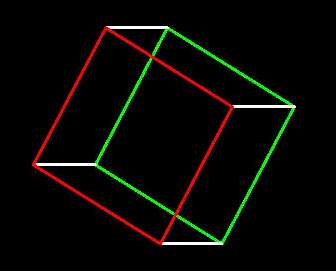

(To color the faces of the 3-cube on your viewer, click the cells... button, under new cell in the cells dialog click begin, and click on the edges of the face you want until it's colored (click clear if you get the wrong face), then click finish. Click begin again to highlight another face, click clear all to start all over. See here for an explanation of this facility. Or you can just do this. Note that you can't do this reliably with the 4-cube at this point, since every edge you see is really two, with the same x, y, and z values, but different w (see below), and the program doesn't know which you mean to click on.)

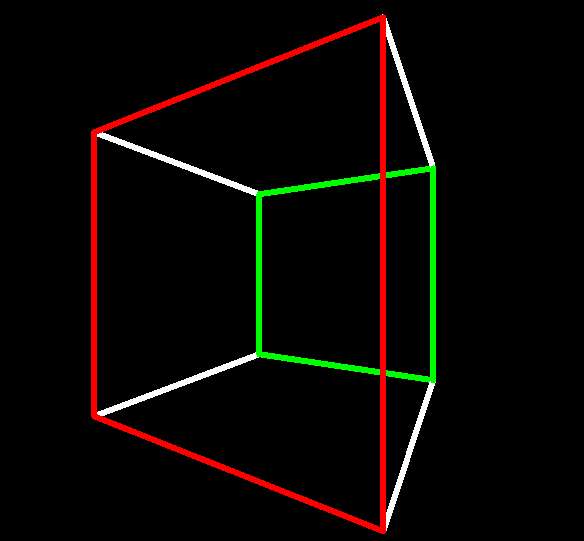
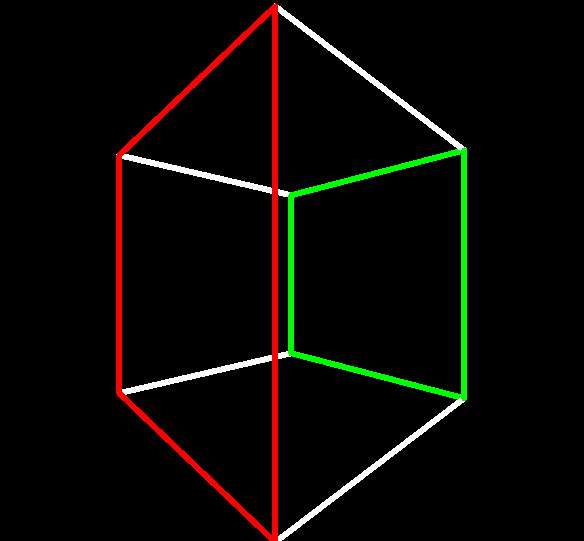
A 3-cube in fact has three pairs of opposite faces thus connected, the other two being:

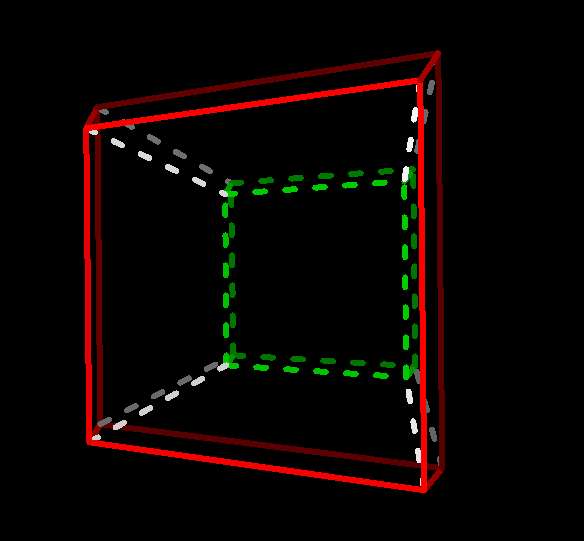
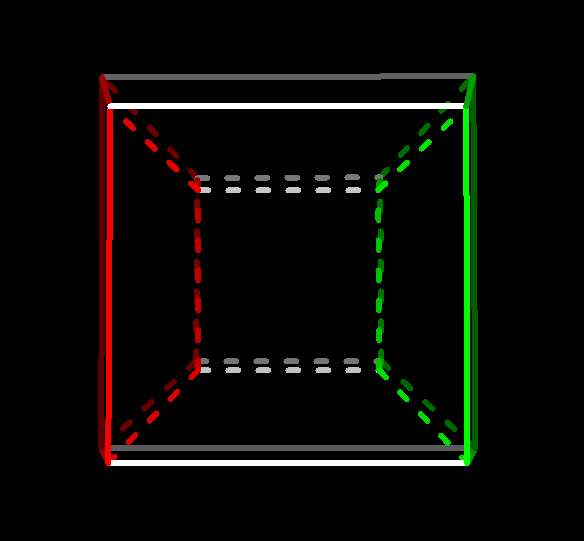
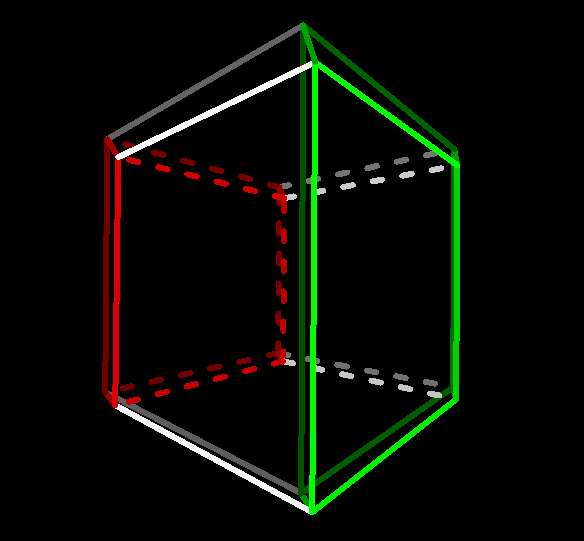
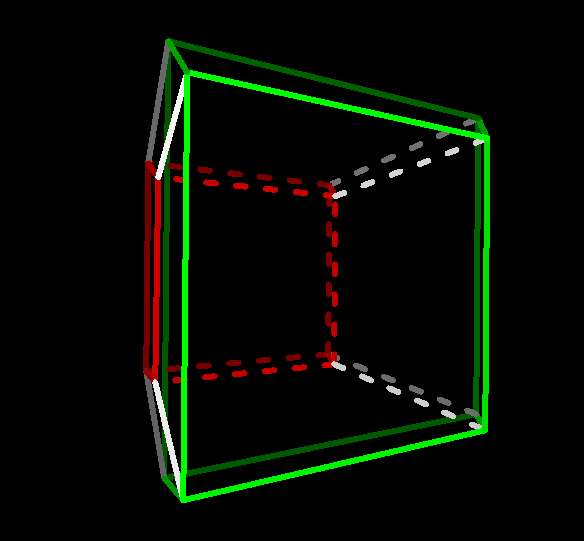
The 3-cube's story ends there, but the 4-cube, which you should have looking pretty much like the above without the colors, still has a set of edges hidden, running in a fourth direction I label w. To see them, rotate the 4-cube with yw to give them a y component:

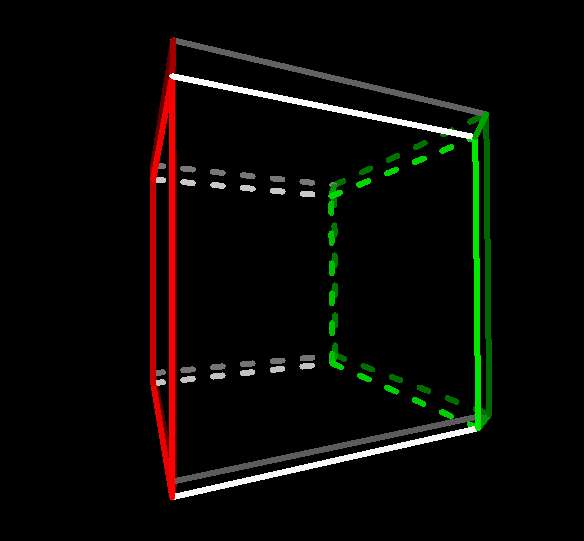
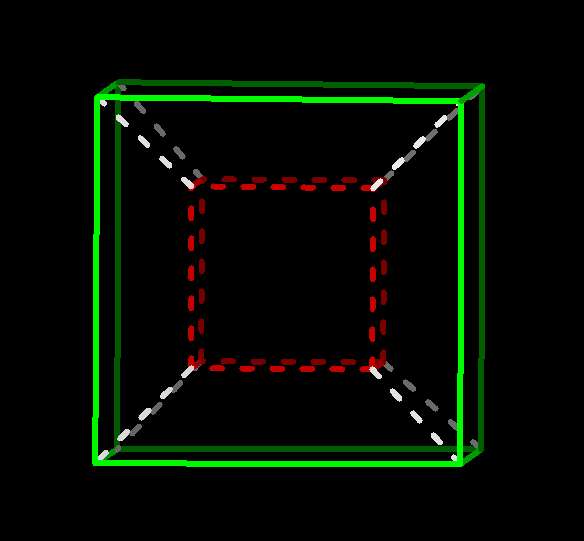
4-cube after yz-rotation

Now you're seeing the entire 4-cube. To make some sense of this confusing figure, notice that it can be seen as two copies of the 3-cube we were just seeing, that were superimposed and are now displaced vertically and connected by the newly-visible w-edges:

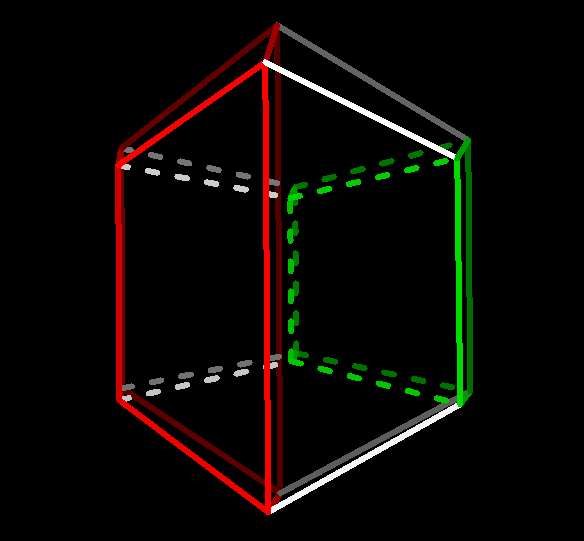
4-cube with opposite facets highlighted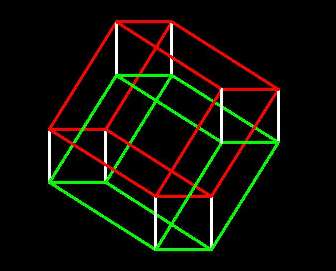

Analogous to the 3-cube and its square faces, the 4-cube has four pairs of opposite 3-cube "facets". They do the same job, forming the boundary of the four-cube, separating its interior and exterior. It's a good exercise to find the other three pairs yourself (use cells...!), or look here.

3-d perpendicular projection onto xy plane
 

To study four-dimensional polytopes that live in xyzw-space, we project them down to familiar xyz-space, and then project that three-dimensional figure onto the xy-space of the viewscreen. With perspective turned off, the projection is perpendicular, as above in the 3d-to-2d case. An important point is that rotations that involve only the dimensions of the space we're projecting to don't essentially change the projected figure - they only rotate it. For 3d-to-2d this is particularly simple:

xy-rotation gives a congruent xy projection

We'll take the same idea one dimension higher. To get a better sense of how the xyz-projection sits in 3-space, click options..., then under both polytope exterior and polytope interior check z-shading, and under polytope interior press dash. Working with the default 4-cube, starting from reset all and pressing xy, xz, yz, and xw briefly will give something like this:

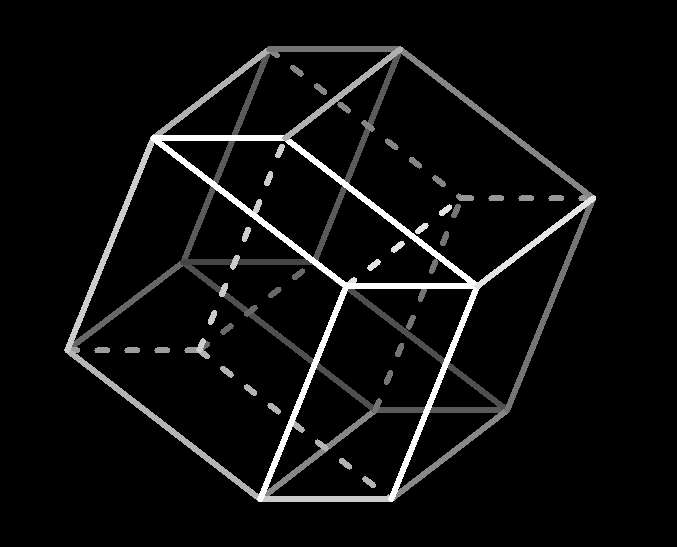Consider that the 4-cube has been perpendicularly projected to our familiar xyz-space, where x and y are the respective horizontal and vertical dimensions of the screen and z runs from you toward the screen. Edges are shaded more dimly the farther they are from you in the z direction, and edges in the interior of the xyz-projection are dashed (in 4-space itself, the 4-cube has no interior edges, any more than a 3-cube in 3-space does). Now try any of xy, xz, and/or yz, and notice that you have essentially the same 3-d figure. Just as with the case of 3d-to-2d projection, applying rotations that involve only x, y, and z to a 4-d figure only rotate its xyz-projection without otherwise changing it; all angles and lengths remain the same, interior edges remain interior and exterior remain exterior. (Tip: you can also rotate the figure in xyz-space by clicking-and-dragging with your mouse. To rotate in xyw-space press Shift while dragging.)

Starting from that same figure and pressing yw (actually Ctrl- or right-clicking: remember, this just reverses the direction of rotation) eventually effects the following transformation:

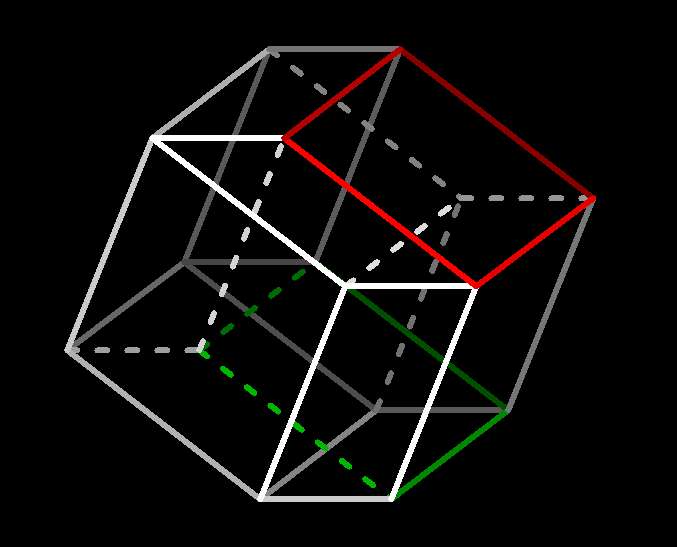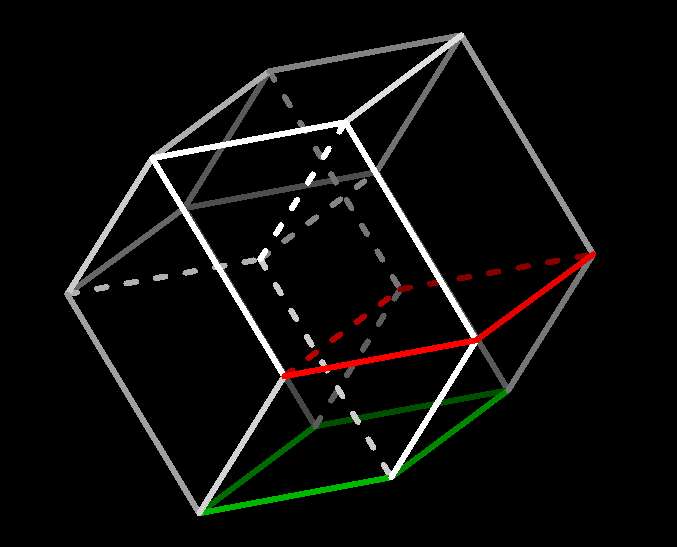yw-rotation essentially changes the xyz projection

Here the xyz-projection has changed essentially: for instance some edges have moved from exterior to interior, and vice-versa.

Finally, let's get a sense of what is happening with rotations that involve w. We first introduce the notion of perspective projection. In the 3d-to-2d case, I call it z-perspective; it's standard and the following diagram illustrates it:

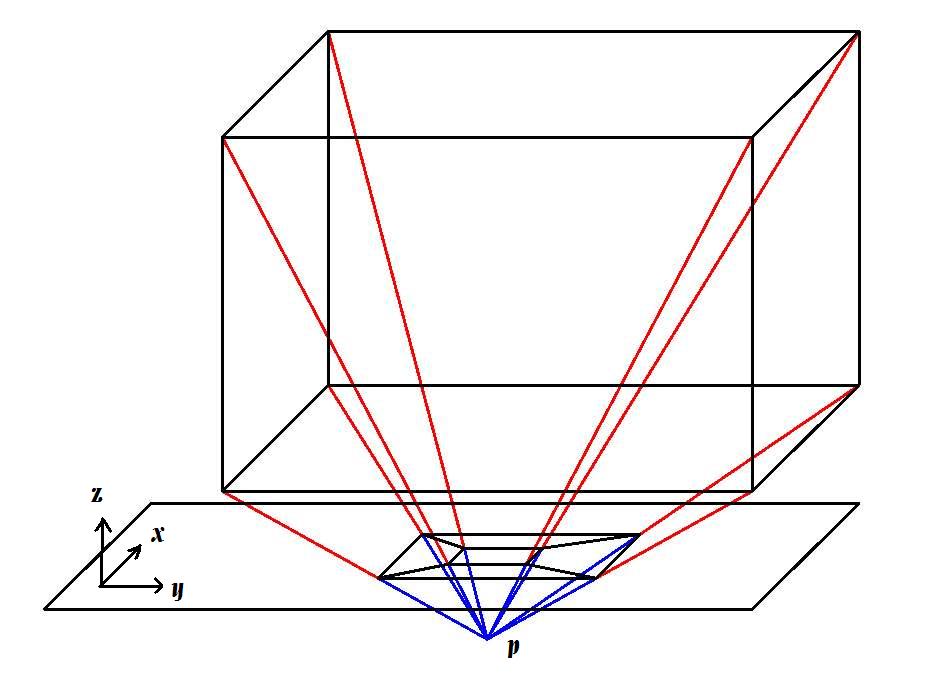standard "z-perspective" projection of 3-cube in initial orientation
 

We place a viewpoint p so that the cube is "in front of" p, i.e., the cube lies in the positive z direction from p, and place a projection plane parallel to the xy-plane between p and the cube ¹. Rays are traced from p to each point of the figure, and where that ray crosses the projection plane is that point's projection. As shown in the diagram, the face of the 3-cube closest to p in the z direction projects to a square and the farthest one projects to a smaller square inside it.

3-cube, initial position, z-perspective		4-cube, (near) initial position, w-perspective
xz-rotation begins		xw-rotation begins
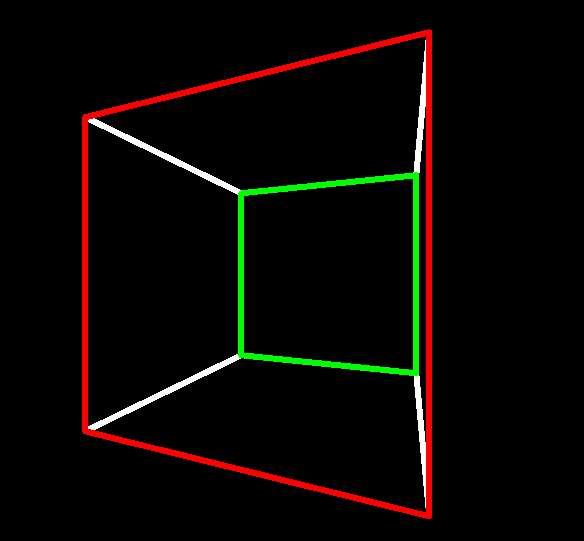
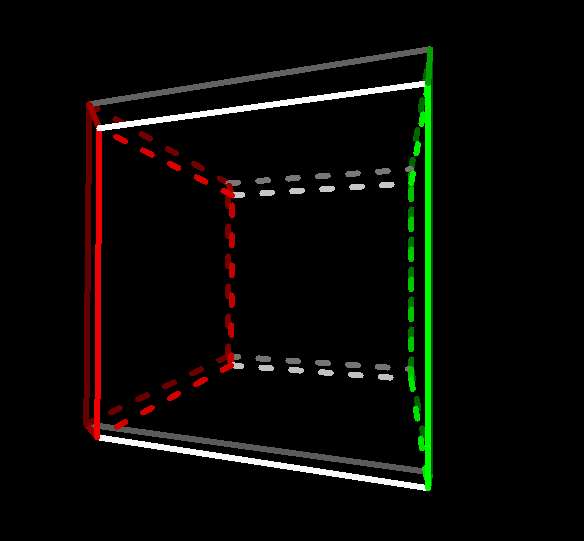
~45° : Red face's trailing edge's closest approach to, and green face's trailing edge's farthest retreat from, p		Red facet's trailing faces's closest approach to, and green facet's trailing face's farthest retreat from, q
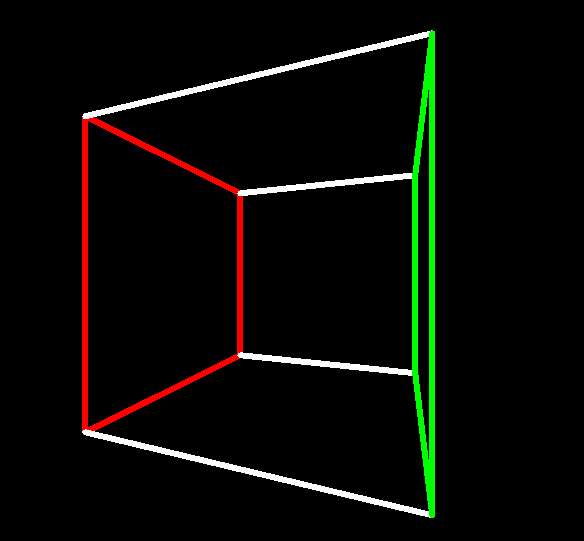
Red face about to turn inside out		Red facet about to do the same
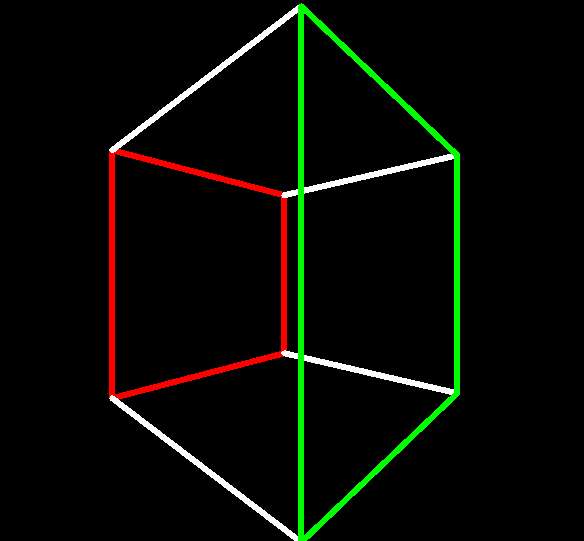
90° : Equipoise!
Green face about to turn inside out		Green facet ditto
~135° : Red face's leading edge's farthest retreat from, and green face's leading edge's closest approach to, p		Red facet's leading face's farthest retreat from, and green facet's leading face's closest approach to, q
180° : Tables turned

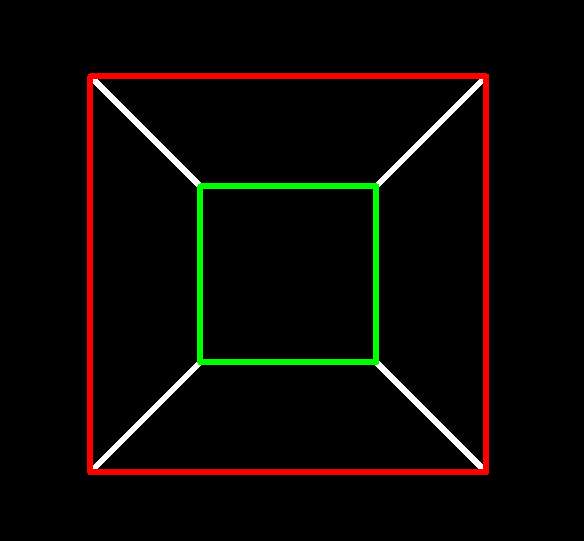
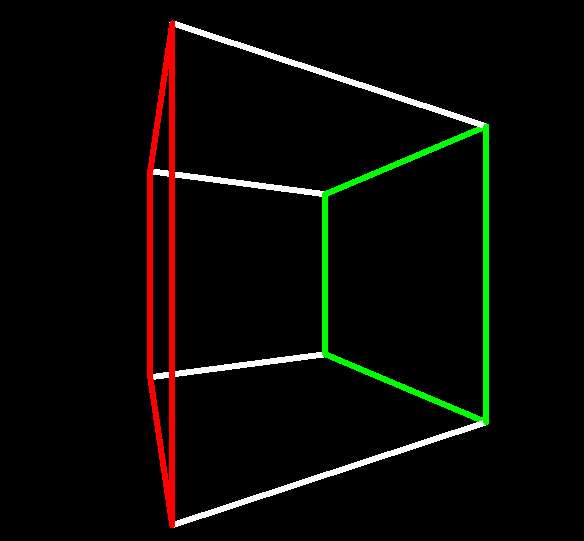
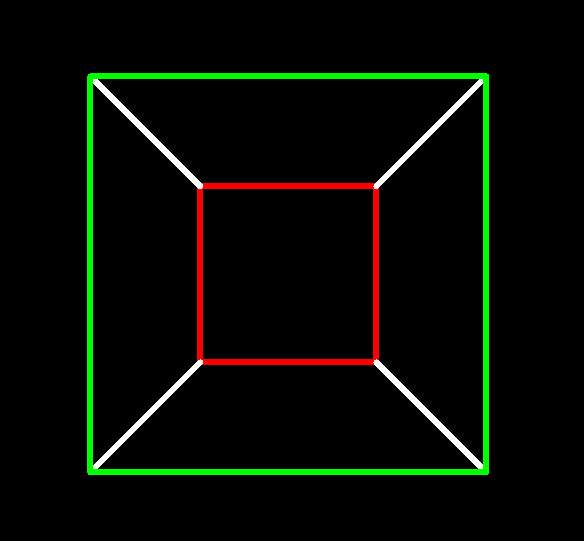
One can use an analogous (and again, standard) method to project a 4-cube from xyzw-space to xyz-space, which I call w-perspective. One places a viewpoint q so that the 4-cube lies in the positive w direction from (i.e. "in front of") it, places a 3-dimensional xyz hyperplane in front of q, traces rays from q to the points of the figure, and projects each point to where its ray crosses the hyperplane. Comparing a 3-cube shown in z-perspective and 4-cube shown in w-perspective, both in initial position (jostling the 4-cube slightly so as to be able to see it all), we see that the 4-cube's projection has a (3-)cube-within-a-cube corresponding to the 3-cube's square-within-a-square. The outer-projecting 3-cube facet (shown in red) is the one closest to q in the w direction, the inner-projecting one (shown in green) is the farthest.

Now to the rotation. First understand that with xw-rotation every point's x and w coordinates are changing in exactly the way that x and y change when you do an xy-rotation, viz. rotate something about the z-axis in 3-space, and the other coordinates don't change at all ². The w dimension is no different than any of the others, it was just unlucky enough to arrive last. Rotate the 3-cube with xz and the 4-cube with xw. Even though the faces of the 3-cube are all the same fixed size, as the red and green rotate to each other's former positions, the first's 2-d projection (eventually) shrinks and the second's grows, and both exchange their own inside and outside. Not remarkable for us since we innately understand that the actual sizes and angles are fixed and automatically interpret projected size as an indicator of z-distance. The trick is to see the relationship between the 3-cube's rotation and its 2-d projection, and understand that the same thing is happening with the 4-cube and its 3-d projection: in the full 4-dimensional hypercube all edges are the same length and all angles are right angles, but in the projected 3-space figure, those lengths (and so necessarily the angles) change according to each edge's w-distance from the viewpoint q. A simple rotation in 4-space causes the 3-space projection to turn inside out.

You can also find discussion and animations of this phenomenon here, with an artist's viewpoint and the math shown explicitly if you want it.

• For tips and tricks with rotations, see here (i.e. RTFM :-)
• Wherever it makes sense, e.g. with rotations and zooming, right- or Ctrl- click the control for reverse action.
• Click options... to try different rendering options. z-shading and using dash or color to distinguish between the projected figure's interior and exterior can help you see how the xyz projection sits in 3-space.
• Try marking or labelling different parts of the figure with vertex labelling, edge coloring, and/or d-cell coloring so that you can follow them as the polytope rotates.

1. Actually, since we can extend the rays forever, we can place the plane anywhere in front of p, not necessarily between p and the figure: in practice the plane is usually conceived as being a fixed distance in front of p as p or the viewed objects move, equivalent to using a camera lens with a fixed focal length. 1
2. The notion of rotation about an axis, so natural and useful in 3-space, doesn't carry over at all to higher dimensions. (In fact in 4-space there is no such thing. Consider a 4-space "general rotation" R, by which I mean a transformation where the origin is left fixed, all distances (and hence all angles) are preserved, and "orientation is preserved", i.e. no mirror images - a so-called "special orthogonal transformation". If R leaves an axis fixed it must leave a whole plane fixed, for the very reason that the only "general rotations" in 3-space are simple rotations about an axis. The difference is that a general rotation in 4-space may leave no point but the origin fixed. Examples are easy - for instance, follow an xy-rotation with a zw-rotation. The net transformation leaves no point but the origin fixed, since every other point has some non-zero coordinate; one of the two planar rotations will change it and the other will leave it alone.) One could refer to what we call an xy-rotation or a rotation "in the xy-plane" as a rotation "about the zw-plane", but what would be the point? Why not name it with the coordinates where something is actually happening. 2