R Lab Session : Part 3

Testing proportions

Problem : 19 Douglas-fir trees in a stand of 53 have succumbed to a fungal pathogen. Lab tests have suggested that 70% of Douglas fir are immune. Assuming that all trees in the stand are infected and all those that are susceptible have died, test if these data are consistent with the laboratory tests.

> prop.test(19, 53, p=.3, alternative="two.sided")

        1-sample proportions test with continuity correction

data:  19 out of 53, null probability 0.3 
X-squared = 0.6074, df = 1, p-value = 0.4358
alternative hypothesis: true p is not equal to 0.3 
95 percent confidence interval:
 0.2349203 0.5025337 
sample estimates:
        p 
0.3584906

Problem : Western red cedar is being tested for vulnerability to the same pathogen. In an infected stand of 39 cedar trees, 5 have died. Test if susceptibility is the same between the two tree species.

> prop.test(c(19,5),c(53,39),p=NULL,alternative="two.sided")
2-sample test for equality of proportions with continuity correction
data:  c(19, 5) out of c(53, 39) 
X-squared = 5.0427, df = 1, p-value = 0.02473
alternative hypothesis: two.sided 
95 percent confidence interval:
0.04166461 0.41890626 
sample estimates:
   prop 1    prop 2 
0.3584906 0.1282051

Exercises : Repeat the first problem using the exact binomial test, binom.test, instead. Does the answer differ? How and why? Also test the hypothesis that 80% of Western red cedar trees are immune.

Paired 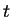$t$ test

Problem : Weights of 9 students (in lbs) before and after a month-long training schedule are given below. Test if the mean weight after training is smaller than the mean weight before training.

 
pre-training:
124 152 129 144 150 153 138 161 140
post-training: 
133 145 131 150 164 132 130 156 141

Copy the two vectors above and save as text files, say pre.txt and post.txt.

> pre <- as.numeric(scan("C:/pre.txt", what="numeric"))
Read 9 items
> post <- as.numeric(scan("C:/post.txt", what="numeric"))
Read 9 items
> weight <- cbind(pre,post)
> t.test(weight[,1],weight[,2],paired=T,conf.level=.95,alternative="greater")

        Paired t-test

data:  weight[, 1] and weight[, 2] 
t = 0.2847, df = 8, p-value = 0.3915
alternative hypothesis: true difference in means is greater than 0 
95 percent confidence interval:
 -5.530518       Inf 
sample estimates:
mean of the differences  1

Note : the difference in means is mean(pre) - mean(post) Perform the same test when the only interest is to see if there is any change.

 

> t.test(weight[,1],weight[,2],paired=T,conf.level=.95,alternative="two.sided")

        Paired t-test

data:  weight[, 1] and weight[, 2] 
t = 0.2847, df = 8, p-value = 0.783
alternative hypothesis: true difference in means is not equal to 0 
95 percent confidence interval:
 -7.09842  9.09842 
sample estimates:

mean of the differences 
                      1

Paired 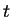$t$ test : sample size calculation

Suppose, for the same problem, it is known from past experience that the standard deviation of the difference in weights is 10 lbs. What should be the minimum sample size necessary to detect a 15 lbs weight change with proability 0.9 ?

 

> power.t.test(delta=15,sd=10,type="paired",alternative="two.sided",power=.9) 
Paired t test power calculation 
n = 6.869959 
delta = 15 
sd = 10 
sig.level = 0.05 
power = 0.9 
alternative = two.sided 
NOTE: n is number of *pairs*, sd is std.dev. of *differences* within pairs

Suppose you have only 5 observations and are interested in testing the hypothesis that there is a difference in mean weights. What would be the power for detecting an effect of size 0.8? (Recall : effect size $(\delta) = \frac{\mu - \mu_0}{\sigma}$)

 

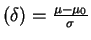> power.t.test(n=5,delta=.8,type="paired",alternative ="two.sided") 
Paired t test power calculation 
n = 5 
delta = 0.8 
sd = 1 
sig.level = 0.05 
power = 0.2806895 
alternative = two.sided

Exercise : What if the level of significance is 1% instead of 5% ?

Two sample 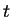$t$ test

Problem : Using the kfm data from R Lab 1, we want to know if there is a difference in birth weight by gender, assuming that weights of boys and girls have the same standard deviation. First you will need to go to R Lab 1, click on the kfm link, and save the data file as text.

  
> kfm <- read.table("C:/kfmdata.txt",header=T)
> kfm
> t.test(weight~sex,data=kfm,type="two.sample",alternative="two.sided",var.equal=T)

        Two Sample t-test

data:  weight by sex 
t = 1.5626, df = 48, p-value = 0.1247
alternative hypothesis: true difference in means is not equal to 0 
95 percent confidence interval:
 -0.06848806  0.54616806 
sample estimates:
 mean in group boy mean in group girl 
           5.43816            5.19932

Do the same dropping the assumption of equal variance for the groups.

> t.test(weight~sex,data=kfm,type="two.sample",alternative="two.sided",var.equal=F)
 
        Welch Two Sample t-test

data:  weight by sex 
t = 1.5626, df = 47.383, p-value = 0.1248
alternative hypothesis: true difference in means is not equal to 0 
95 percent confidence interval:
 -0.06859144  0.54627144 
sample estimates:
 mean in group boy mean in group girl 
           5.43816            5.19932

Exercise : If you know that the s.d. = 0.5 lb for both the groups and the two samples have the same size (say 25), what would be the power for detecting a difference in mean of 0.5 lb?

Wilcoxon-Mann-Whitney Test

Problem : Ms. Whitmore has been handing out lollypops for Halloween. At the beginning of the evening, she is very generous, but as the evening wears on she begins to fear for her lollypop supply and becomes stingier. The numbers given below are counts of lollypops given to each child. Test the hypothesis that the average number of lollypops received by a child is 6.

26 18 20 25 19 23 14 12 15 10 8 7 5 2 3 2 2

Copy the data and save it as a text file.

> lolly <- as.numeric(scan("C:/lolly.txt", what="numeric"))
> qqnorm(lolly)
> wilcox.test(lolly, exact=F, mu=6, alternative="two.sided")

        Wilcoxon signed rank test with continuity correction

data:  lolly 
V = 128, p-value = 0.01561
alternative hypothesis: true mu is not equal to 6

Problem : Percent ground area covered by moss has been measured in two different arctic tundra types, in twelve plots in each, data given below. Do the two tundra types differ in moss cover?

> ws <- c(0, 2, 3, 8, 5, 12, 24, 53, 6, 79, 19, 61)
> tt <- c(13, 9, 58, 17, 49, 71, 39, 10, 89, 54, 26, 75)
> qqnorm(ws)
> qqnorm(tt)
> wilcox.test(ws,tt,paired=F,alternative="two.sided")

        Wilcoxon rank sum test

data:  ws and tt 
W = 37, p-value = 0.0449
alternative hypothesis: true mu is not equal to 0

Exercises : Using the kfm data, test the hypothesis that maternal weight differs between mothers who give birth to boys vs. girls.



The data below represent counts of dental cavities detected in the children who visited Ms. Whitmore on Halloween. The first row is from dental examinations six months prior to Halloween, the second from six months after. Is there evidence of an increase in cavities? If so, does this necessarily implicate Ms. Whitmore, or, for that matter, Halloween?

1 0 3 1 2 0 1 3 0 0 4 2 0 1 1 0 2

2 0 1 1 0 1 2 0 1 0 2 3 3 2 1 1 0

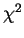$\chi^2$ Test

The Chi-squared test has not been covered yet in class, but it is another one you will need to know how to use. Enter

 
>help(chisq.test)

to see a description of this test and the parameters it takes. You can use this command for an explanation of any of the tests here. To see a full list of tests available in R, enter data: obs

 >help(package=ctest)

. Snapdragon Example (from Book) Test whether data fit the model of probabilities 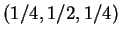$(1/4,1/2,1/4)$ for (white, pink, red), respectively.

> obs<-c(54,122,58)
> nullprob<-c(.25,.5,.25)
> chisq.test(obs,p=nullprob)

        Chi-squared test for given probabilities

X-squared = 0.5641, df = 2, p-value = 0.7542

For a 2-way test, you just enter in the contingency table:

> data(HairEyeColor) #Brings in data set that's in R
> malecolor<-HairEyeColor[,,1] #Just brings the males' 
(3-diminsional array)-- don't worry about understanding
> malecolor
       Eye
Hair    Brown Blue Hazel Green
  Black    32   11    10     3
  Brown    38   50    25    15
  Red      10   10     7     7
  Blond     3   30     5     8
> chisq.test(malecolor)

        Pearson's Chi-squared test

data:  malecolor
X-squared = 42.1633, df = 9, p-value = 3.068e-06

Warning message: 
Chi-squared approximation may be incorrect in: chisq.test(malecolor)

Exercise (Good for Homework!) Bring in the graft dataset on web and do a 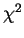$\chi^2$ test for independence - hint use table( ) to get in the contingency table format. (type is the type of leukaemia: Acute Myeloid, Acute Lymphatic, and Chronic Myeloid; gvhd is whether patient developed graft-versus-host disease)