


Next: About this document ...
R Lab Session : Part 2
To see a review of how to start R, look at the beginning of
Lab1
Probability Calculations
The following examples demonstrate how to calculate the value of the
cumulative distribution function at (or the probability to the left
of) a given number.
- Normal(0,1) Distribution :
> x <- c(-2,-1,0,1,2)
> x
[1] -2 -1 0 1 2
> pnorm(x)
[1] 0.02275013 0.15865525 0.50000000 0.84134475 0.97724987
- Binomial(
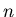 ,
,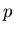 ) Distribution :
) Distribution :
> x <- c(0,1,2,5,8,10,15,20)
> pbinom(x,size=20,prob=.2)
[1] 0.01152922 0.06917529 0.20608472 0.80420779 0.99001821 0.99943659 0.99999999
[8] 1.00000000
- Poisson(
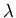 ) Distribution :
) Distribution :
> x <- c(0,1,2,5,8,10,15,20)
> ppois(x,6)
[1] 0.002478752 0.017351265 0.061968804 0.445679641 0.847237494 0.957379076
[7] 0.999490902 0.999998545
Exercise : Calculate the following probabilities :
- 1.
- Probability that a normal random variable with mean 22 and
variance 25
- (i)
- lies between 16.2 and 27.5
- (ii)
- is greater than 29
- (iii)
- is less than 17
- (iv)
- is less than 15 or greater than 25
- 2.
- Probability that in 60 tosses of a fair coin the head comes
up
- (i)
- 20,25 or 30 times
- (ii)
- less than 20 times
- (iii)
- between 20 and 30 times
- 3.
- A random variable X has Poisson distribution with mean
7. Find the probability that
- (i)
- X is less than 5
- (ii)
- X is greater than 10
- (iii)
- X is between 4 and 16
Quantiles
The following examples show how to common the quantiles of some
common distributions for a given probability (or a number between
0 and 1).
- Normal(0,1) Distribution :
> y <- c(.01,.05,.1,.2,.5,.8,.95,.99)
> qnorm(y,mean=0,sd=1)
[1] -2.3263479 -1.6448536 -1.2815516 -0.8416212 0.0000000 0.8416212 1.6448536
[8] 2.3263479
- Binomial(
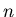 ,
,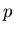 ) Distribution :
) Distribution :
> y <- c(.01,.05,.1,.2,.5,.8,.95,.99)
> qbinom(y,size=30,prob=.2)
[1] 1 3 3 4 6 8 10 11
- Poisson(
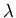 ) Distribution :
) Distribution :
> y <- c(.01,.05,.1,.2,.5,.8,.95,.99)
> qpois(y,6)
[1] 1 2 3 4 6 8 10 12
Random Variable generation
The following examples illustrate how to generate random samples from
some of the well-known probability distributions.
Exercise (Advanced) : Generate 500 samples from Student's 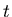 distribution
with 5 degrees of freedom and plot the historgam. (Note:
distribution
with 5 degrees of freedom and plot the historgam. (Note: 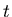 distribution is going to be covered in class). The corresponding
function is rt .
distribution is going to be covered in class). The corresponding
function is rt .
Density Plots
- Plotting the probability density function (pdf)
of a Normal distribution :
> x11()
> x <- seq(-4.5,4.5,.1)
> normdensity <- dnorm(x,mean=0,sd=1)
> plot(x,normdensity,type="l")
- Plotting the probablity mass function (pmf) of a Binomial
distribution :
> par(mfrow=c(2,1))
> k <- c(1:30)
> plot(k,dbinom(k,size=30,prob=.15),type="h")
> plot(k,dbinom(k,size=30,prob=.4),type="h")
> par(mfrow=c(1,1))
- Discrete Probabilities For a discrete random variable, you can use the probability mass to find
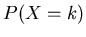
> dbinom(3,size=10,prob=0.5)
[1] 0.1171875
** Note the distinction between the continuous (Normal)
and the discrete (Binomial) distrubtions.
Exercise : Plot the probability mass functions for the
Poisson distribution with mean 4.5 and 12 respectively. Do you see any
similarity of these plots to any of the plots above? If so, can you
guess why ?
Exercise : Recreate the probabilities that Professor Holmes did in class (Bin(5,.4)) [You can do it in 1 command!] How would you get the expected counts?
Q-Q plot
R has two different functions that can be used for generating a
Q-Q plot. Use the function qqnorm for plotting sample quantiles
against theoretical (population) quantiles of standard normal random variable.
Example :
> stdnormsamp <-rnorm(100,mean=0,sd=1)
> normsamp <- rnorm(100,mean=5,sd=1)
> binomsamp <-rbinom(100,size=20,prob=.25)
> poissamp <- rpois(100,5)
> par(mfrow=c(2,2))
> qqnorm(stdnormsamp,main="Normal Q-Q plot : N(0,1) samples")
> qqline(stdnormsamp,col=2)
> qqnorm(normsamp,main="Normal Q-Q plot : N(5,1) samples")
> qqline(normsamp,col=2)
> qqnorm(binomsamp,main="Normal Q-Q plot : Bin(20,.25) samples")
> qqline(binomsamp,col=2)
> qqnorm(poissamp,main="Normal Q-Q plot : Poisson(5) samples")
> qqline(poissamp,col=2)
Note: Systematic departure of points from the Q-Q line (the red
straight line in the plots) would indicate some type of departure from
normality for the sample points.
Use of function qqplot for plotting sample quantiles for one
sample against the sample quantiles of another sample
Example :
> par(mfrow=c(2,1))
> qqplot(stdnormsamp,normsamp,xlab = "Sample quantiles : N(0,1) samples",
+ ylab = "Sample quantiles : N(5,1) samples")
> qqplot(stdnormsamp,binomsamp,xlab = "Sample quantiles : N(0,1) samples",
+ ylab = "Sample quantiles : Bin(20,.25) samples")
Exercise : Generate 100 samples from Student's 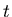 distribution
with 4 degrees of freedom and generate the qqplot for this
sample. Generate another sample of same size, but now from a
distribution
with 4 degrees of freedom and generate the qqplot for this
sample. Generate another sample of same size, but now from a 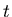 distribution with 30 degrees of freedom and generate the q-q plot.
Do you see any difference ?
distribution with 30 degrees of freedom and generate the q-q plot.
Do you see any difference ?



Next: About this document ...
Elizabeth Purdom
2003-10-13