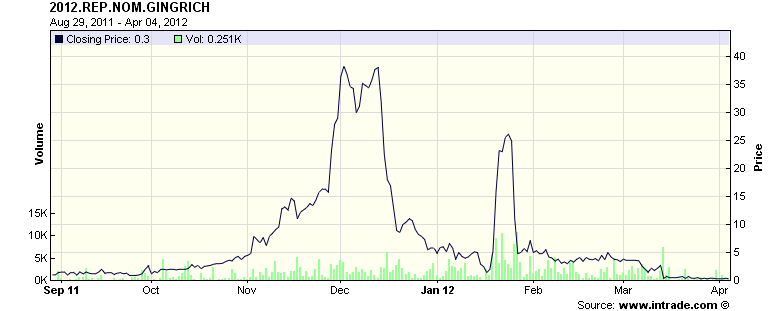
There are several ways to get data on current probabilities of future events, the most accessible being gambling odds and prediction markets. On this page I consider a contest with known contenders where there will be one winner at a known date. The interesting case is where there is no early favorite. I will show data concerning candidates for the Republican Presidential Nomination in 2012 and 2016, and NFL teams competing to be the Superbowl winner in 2015-16 and 2016-17. Here is a typical graph showing prediction market price (probability, as a percent) over time for one contender (here Gingrich for 2012 Nomination) and we see that the maximum was 38, representing a perceived 38% chance of winning the Nomination at that time.

The next table shows these maximum probabilities for each contender whose maximum reached 10%.
| Nomination 2012 | Nomination 2016 | Superbowl 2015-16 | Superbowl 2016-17 |
|---|---|---|---|
| 100 Romney | 100 Trump | 100 Denver | 100 New England |
| 39 Perry | 53 Rubio | 65 Carolina | 41 Atlanta |
| 38 Gingrich | 36 Bush | 31 New England | 18 Dallas |
| 28 Palin | 24 Cruz | 24 Green Bay | 16 Seattle |
| 25 Pawlenty | 23 Walker | 18 Arizona | 16 Green Bay |
| 18 Santorum | 13 Christie | 13 Seattle | 16 Pittsburgh |
| 18 Huntsman | 12 Paul | 10 Cincinnati | 10 Minnesota |
| 18 Bachmann | 12 Carson | 10 Kansas City | |
| 17 Huckabee | 11 Fiorini | ||
| 14 Daniels | |||
| 10 Christie | |||
| 10 Perry |
Remarkably, there is a piece of theory that doesn't depend on the nature of the competition.
Consider a competition with several contenders, and a (prediction market) price for each contender. Suppose initially all these prices are below b, for given 0 < b < 100. Theory says that the mean number of candidates whose price ever exceeds b should equal 100/b.The implicit assumption here is the "wisdom of crowds" assumption that the "consensus estimate of probability" obtained from the market does reflect true probabilities, and that the standard mathematical formulation of probability theory does apply to real world future events.
The conceptual point is that, while simple math can't tell you the actual probabilities, it does make some testable predictions about how probabilities should change with time. And these predictions are fairly accurate. This conceptual point is different from (though in the same spirit as) the conceptual point from the prediction tournament discussion: one can assess people's relative abilities to estimate probabilities, even when true probabilities are unknown.
My own more detailed account of this topic appears in this published paper and these lecture notes.