STAT 244 ASSIGNMENT 3 SPRING, 2011

due 4/15/11

1 ARMA Parameter Estimation

Generate five sequences of 1000 observations from five different ARMA processes with parameters of your choice, using different small values for p and q and different ARMA parameters for each of the five sequences. You can use the routines available in the ts library of R to generate the necessary sequences of observations, or you can generate them based on the definition of an ARMA process. (Alternatively, use ``real'' data sets of your choice instead of one or more of the five sequences.) Write a program to estimate the parameters of the ARMA process using the Kalman filter. Programs for evaluating the likelihood of an ARMA process are available in ~s244/as/as154.f, and can be accessed either by compiling them directly, or using the s244 library (-ls244). Your program should be written to be able to switch between at least two different maximization algorithms from among Powell's method, the downhill simplex (Nelder and Mead), and other algorithms. The programs for Powell's method can be found in the directory ~s244/nr , on the class webpage, and are also available via -ls244. (These programs are direct transcriptions from the book ``Numerical Recipes in C'', except that floats have been converted to doubles, the one-based arrays have been converted to zero-based arrays, and function arguments have been updated to the ANSI standard.) Compare the performance of the minimization routines you choose, especially when the program is presented with bad guesses for the initial values, with regard to execution time and number of function evaluations.

2 Autocovariance using the Fast Fourier Transform

Using one of the data sets which you generated in part 1, calculate the first 20 autocovariances for the sequence, first by the basic formula, i.e.:

$$C(k)={1 \over N }\sum_{t=1}^{N-k} (X_t-\bar X) (X_{t+k}-\bar X)\qquad k=1,\ldots,20$$

and then by using the Fast Fourier Transform (FFT). Estimate the relative execution times you would expect for the two methods based on an analysis of the algorithms, and then compare the actual execution times. How would the relative efficiencies change if you desired to calculate the first 50 autocovariances instead of the first 20? You can determine this either by analysis of the algorithms, or by computer timing.

About this document ...

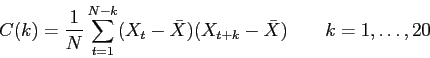
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 0 -link 0 -show_section_numbers a3.tex

The translation was initiated by Phil Spector on 2011-01-18